Z analizy testów CKE przeprowadzonej przez nauczycieli Firmy "MARKA", wynika, iż pewne zagadnienia w testach egzaminacyjnych w latach 2002-2008 pojawiały się w częściej niż inne. Wielce prawdopodobne, że i w tym roku można spodziewać się tego typu tematów tzw. "pewniaków".
- umiejętność sprawnego wykonywania działań arytmetycznych na liczbach rzeczywistych (dodawania, odejmowania, mnożenia i dzielenia ułamków zwykłych i dziesiętnych)
Przykład:
Masa kości szkieletu ciała ludzkiego wynosi 9800 g. Jaka jest (w przybliżeniu) całkowita masa tego człowieka, jeżeli wiadomo, że masa szkieletu stanowi 0,17 masy całego ciała?Odpowiedź: 57,6 kg.
- umiejętność operowania procentami w rozmaitych sytuacjach praktycznych
Przykład:
W Kampinoskim Parku Narodowym lasy zajmują powierzchnię 27 tys. ha, zaś w Tatrzańskim Parku Narodowym – powierzchnię 15,2 tys. ha. O ile procent więcej lasów jest w Puszczy Kampinoskiej niż w Tatrach?Odpowiedź: O około 78%.
- umiejętność odczytywania informacji przedstawionych w rozmaitych formach (tabeli, diagramu, rysunku) i przetwarzania tych informacji
Przykład:
Oto wyniki krótkiego sprawdzianu przeprowadzonego w trzech oddziałach III klasy gimnazjum:


Z wykresów tych wynika, że sprawdzian był:
A. najtrudniejszy dla uczniów z III a
B. najtrudniejszy dla uczniów z III b
C. najtrudniejszy dla uczniów z III c
D. jednakowo trudny dla uczniów ze wszystkich trzech klasOdpowiedź: A.
- umiejętność przekształcania wyrażeń algebraicznych
Przykład:
Ze wzoru opisującego pole powierzchni prostopadłościanu: P=2(ab+bc+ac) wyznacz a.Odpowiedź:
 .
. - umiejętność zapisania treści zadania za pomocą układu równań oraz rozwiązania tego układu równań (czyli tzw. "zadania tekstowe")
Przykład:
W III klasie pewnego gimnazjum przeprowadzony został test. Test zawierał 100 pytań; za prawidłową odpowiedź uczeń otrzymywał 2 punkty, za złą (-1) punkt, a za brak odpowiedzi 0 punktów. Po sprawdzeniu testu okazało się, że uczeń nie udzielił 20 odpowiedzi i łącznie uzyskał 100 punktów. Ile było odpowiedzi dobrych, a ile błędnych?Odpowiedź: 60 dobrych i 20 błędnych.
- umiejętność posługiwania się własnościami figur geometrycznych i rozpoznawania symetrii
Przykład:
Na zabawę przygotowano ciastka o różnych kształtach. Które ciastka mają dokładnie 5 osi symetrii?
A. 2 i 3
B. 3 i 4
C. 4 i 5
D. 3 i 5Odpowiedź: B.
- umiejętność stosowania twierdzenia Pitagorasa
Przykład:
Trawnik ma kształt czworokąta, jak na rysunku: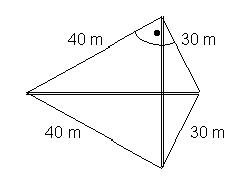
Jaką długość mają przecinające trawnik ścieżki (zaznaczone na rysunku podwójnymi liniami)? Odpowiedź: 48 cm i 50 cm.
- umiejętność obliczania obwodów i pól powierzchni figur płaskich
Przykład:
Pień starego dębu ma na pewnej wysokości obwód 6,3 m. Jaka jest średnica pnia? (Wynik podaj z dokładnością do 10 cm).Odpowiedź: 200 cm.
- umiejętność obliczania objętości i pól powierzchni brył
Przykład:
Do prostopadłościennego akwarium o wymiarach 5 dm × 30 cm × 25 cm, całkowicie wypełnionego wodą, włożono sześcienną ołowianą kostkę, której pole powierzchni całkowitej wynosi 600 cm². Ile litrów wody pozostało w akwarium po wrzuceniu kostki?Odpowiedź: 36,5 litra.
- umiejętność stosowania tzw. "technik twórczego rozwiązywania problemów" (czyli samodzielne sformułowanie hipotezy – lub wybranie jednej z przedstawionych hipotez – i próba jej uzasadnienia)
Przykład:
Na gałązce świerku każdego roku wyrastają z nowego pąka 3 nowe pędy zakończone pąkiem. Ile pąków będzie miała po dziewięciu latach świerkowa gałązka, która wyrosła z jednego pąka?A. 3·9
B. 3+9
C. 9³
D. 39Odpowiedź: D.
Opracował mgr Krzysztof Zawadzki – nauczyciel Firmy "MARKA"
Sprawdź kursy przygotowawcze w Warszawie – www.marka.edu.pl
Z analizy testów CKE przeprowadzonej przez nauczycieli Firmy „MARKA”, wynika, iż pewne zagadnienia w testach egzaminacyjnych w latach 2002-2012 pojawiały się w częściej niż inne. Wielce prawdopodobne, że i w tym roku można spodziewać się tego typu zadań.
- znajomość pojęcia skali mapy, umiejętność posługiwania się skalą mapy do obliczania odległości w terenie
Przykład:
Dwie miejscowości oddalone są od siebie o 5 km. Ich odległość na mapie wynosi 10 cm. Jaka jest skala tej mapy?
A. 1 : 100.000
B. 1 cm — 1,5 km
C. 1 : 50.000
D.
Odpowiedź: C. - umiejętność obliczania powierzchni za pomocą skali mapy
Przykład:
Działka, na której stoi dom państwa Kowalskich, ma kształt prostokąta o wymiarach 40 m × 50 m. 12% tej działki zajmuje dom, a reszta stanowi ogródek. Sporządzono plan tej działki. Na tym planie powierzchnia ogródka wynosi 1760 cm². Jaka jest skala planu?Odpowiedź: 1 : 100.
- znajomość pojęcia czasu miejscowego (słonecznego) i umiejętność wyznaczania go na podstawie długości geograficznej
Przykład:
W Warszawie (21°E) jest godzina 6.00 czasu miejscowego. Która godzina czasu miejscowego jest w Nowym Jorku (74°W)?Odpowiedź: 23:40.
Opracował mgr Krzysztof Zawadzki – nauczyciel Firmy „MARKA”
Sprawdź kursy przygotowawcze w Warszawie – www.marka.edu.pl
Z analizy testów Centralnej i Okręgowych Komisji Egzaminacyjnych przeprowadzonej przez nauczycieli Firmy "MARKA", wynika, iż pewne zagadnienia w testach egzaminacyjnych w ostatnich latach pojawiały się w częściej niż inne. Wielce prawdopodobne, że i w tym roku można spodziewać się tego typu tematów tzw. "pewniaków".
- odczytywanie z wykresu informacji dotyczących ruchów ciał i przetwarzania tych informacji
Przykład:
Wykres przedstawia prędkość autobusu w zależności od czasu podczas jazdy między dwoma przystankami.

Które z poniższych zdań nie jest prawdziwe?
A. Na odcinkach I i III autobus poruszał się ruchem jednostajnie przyspieszonym.
B. Czas postoju autobusu był równy 50 sekund.
C. Przyspieszenie autobusu na odcinku III było mniejsze niż na odcinku I.
D. Odległość między przystankami była większa niż 9 km. - stosowanie praw ruchu jednostajnego i jednostajnie zmiennego
Przykład:
Z dachu budynku upuszczono kamień, który spadł na ziemię. Czas spadania wynosił 2 sekundy. Każda kondygnacja budynku miała wysokość l=2,80 m. Przyjmujemy, że przyspieszenie ziemskie jest równe g=9,8 m/s2 oraz π=22/7.
Wybierz właściwą odpowiedź:
Budynek ten miał
A. 10 pięter
B. 9 pięter
C. 7 pięter
D. 6 pięter - stosowanie praw ruchu po okręgu
Przykład:
Wokół Ziemi, z prędkością 6050 km/h, krąży na orbicie satelita obiegający Ziemię w czasie 8 godzin.

Odległość orbity satelity od powierzchni Ziemi jest równa
A. 7.700 km
B. 2.400 km
C. 1.300 km
D. 600 km - analizowanie sił działających na ciało
Przykład:

Na balon działają siły: siła ciężkości Fc i siła wyporu Fw, jak na rysunku. Można stwierdzić, że balon ten
A. Opada w dół ze stałą prędkością.
B. Wisi nieruchomo w powietrzu.
C. Wznosi się ze stałą prędkością.
D. Wznosi się z coraz większą prędkością. - znajomość pojęć energii kinetycznej i potencjalnej oraz stosowanie zasady zachowania energii
Przykład:
Turyści wyszli ze schroniska PTTK „Markowe Szczawiny” i wędrując ze stałą przez cały czas prędkością weszli na szczyt Babiej Góry.
Które z poniższych zdań jest prawdziwe?
Podczas tej wędrówki
A. ich energia potencjalna rosła, a energia kinetyczna malała
B. ich energia potencjalna malała, a energia kinetyczna rosła
C. ich energia potencjalna była stała, a energia kinetyczna rosła
D. ich energia potencjalna rosła, a energia kinetyczna była stała. - odczytywanie z wykresu informacji dotyczących ogrzewania ciał i zmian stanu skupienia oraz przetwarzanie tych informacji
Przykład:
Gospodyni zdjęła z kuchenki garnek z wrzącą wodą i wystawiła go na ganek. Był silny mróz.
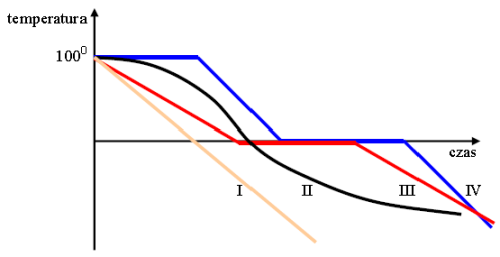
Temperaturę zawartości garnka w zależności od czasu pokazuje wykres:
A. I
B. II
C. III
D. IV - określanie zależności zmian temperatury ciała od ilości dostarczonej lub oddanej energii
Przykład:
Trzy metalowe kule: miedzianą, żelazną i aluminiową, każdą o masie 2 kilogramów, włożono do trzech jednakowych naczyń zawierających wodę zmieszaną z lodem i ogrzewano w jednakowy sposób przez 5 minut. Po tym czasie zmierzono temperaturę wody w naczyniach.
Które z poniższych zdań jest prawdziwe? (Możesz posłużyć się zamieszczoną tabelą ciepła właściwego ciał).Substancja Ciepło właściwe J/ kg . oC rtęć 100 srebro 250 miedź 380 żelazo 460 duraluminium 880 glin 920 A. Temperatura we wszystkich naczyniach była jednakowa. B. Najwyższa temperatura była w naczyniu z kulą aluminiową.
C. Najwyższa temperatura była w naczyniu z kulą żelazną.
D. Najwyższa temperatura była w naczyniu z kulą miedzianą. - analizowanie schematów obwodów elektrycznych
Przykład:
Żarówka włączona do obwodu zbudowanego według poniższego schematu ma oporność 8 Ω .

Wskaż zdanie prawdziwe:
A. Woltomierz wskazuje 24 V, zaś amperomierz 72 A.
B. Woltomierz wskazuje 3 V, zaś amperomierz 24 A.
C. Woltomierz wskazuje 24 V, zaś amperomierz 3 A.
D. Woltomierz wskazuje 24 V, zaś amperomierz 1/3A. - obliczanie pracy prądu przepływającego przez urządzenie elektryczne oraz kosztu zużytej energii elektrycznej
Przykład:
Latarnia przed domem zapala się codziennie o godzinie 1600. Żarówka w latarni ma moc 100 W.W listopadzie koszt zużytej przez latarnię energii elektrycznej wyniósł 13,50 zł. O której godzinie latarnia przed domem gaśnie, jeżeli 1 kWh energii elektrycznej kosztuje 30 groszy? - stosowanie praw optyki
Przykład:
Rysunek przedstawia prawo odbicia światła.

Jeżeli kąt, jaki tworzy promień światła padającego z powierzchnią dzielącą oba ośrodki, zwiększy się o 10°, to kąt między promieniem padającym a promieniem odbitym
A. nie zmieni się
B. zwiększy się o 10°
C. zmniejszy się o 20°
D. nie można tego określić nie znając kątów α i β.
Odpowiedzi
- D
- D
- C
- D
- D
- C
- D
- C
- o godzinie 7:00
- C
{mospagebreak title=z 2006&heading=z 2007}
Z analizy testów CKE przeprowadzonej przez nauczycieli Firmy "MARKA", wynika, iż pewne zagadnienia w testach egzaminacyjnych w latach 2002-2005 pojawiały się w częściej niż inne. Wielce prawdopodobne, że i w tym roku można spodziewać się tego typu tematów tzw. "pewniaków".
- umiejętność przeliczania jednostek różnych wielkości fizycznych
Przykład:
Najszybsze zwierzę na Ziemi – gepard – potrafi biec z prędkością 110 km/h . Ile (w przybliżeniu) metrów przebiegnie w czasie 1 sekundy?Odpowiedź: Około 30 m.
- umiejętność stosowania praw ruchu jednostajnego
Przykład:
W wyścigu kolarskim grupa kolarzy odłączyła się od peletonu i ma do mety jeszcze 95 km. Grupa ta jedzie ze stałą prędkością 38 km/h. Jeśli prędkość kolarzy nie zmieni się, to miną oni linię mety za:A. 30 min
B. 150 min
C. 250 min
D. 300 minOdpowiedź: B.
- umiejętność odczytywania z wykresu informacji dotyczących ruchów ciał i przetwarzania tych informacji
Przykład:
Mateusz wyjechał z domu na rowerze, aby odwiedzić babcię. Wykres przedstawia zależność prędkości Mateusza od czasu.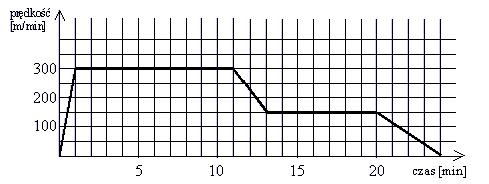
Ile kilometrów przejechał Mateusz w ciągu pierwszych 10 minut?
Odpowiedź: 2,85 km.
- umiejętność stosowania zasad dynamiki Newtona
Przykład:
Tramwaj jedzie po prostych szynach ze stałą prędkością. O siłach działających na tramwaj w kierunku poziomym można powiedzieć, że:
A. siła ciągu silnika i siły oporów są równe co do wartości,
B. wartość siły ciągu silnika jest większa od sił oporów,
C. siły oporów są większe od siły ciągu silnika,
D. nie można jednoznacznie określić, jeśli nie znamy wartości prędkości tramwaju.Odpowiedź: A – zgodnie z I zasadą dynamiki.
- umiejętność obliczania pracy i mocy w sytuacjach związanych z ruchem ciał
Przykład:
Wieloryb płynąc z prędkością 7,5 m/s pokonuje opór wody równy 18 kN. Jaką moc ma wówczas ten wieloryb?Odpowiedź: 135 kW.
- znajomość pojęć energii kinetycznej i energii potencjalnej oraz umiejętność stosowania zasady zachowania energii
Przykład:
Z okna na siódmym piętrze budynku (wysokość około 20 m) wypadła piłka. Z jaką prędkością ta piłka uderzy o ziemię?
Przyjmij przyspieszenie ziemskie g=10 m/s²Odpowiedź: 20 m/s czyli 72 km/h.
- umiejętność odczytywania z wykresu i przetwarzania informacji dotyczących ogrzewania ciał i zmian stanu skupienia
Przykład:
Uczniowie umieścili w naczyniu kawał lodu oraz termometr i ustawili naczynie w ciepłym pokoju. Co minutę mierzyli temperaturę w naczyniu, a otrzymane wyniki przedstawili na wykresie. Wykres ma postać: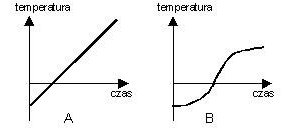
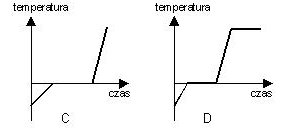
Odpowiedź: D.
- umiejętność stosowania prawa Ohma
Przykład:
Żarówka w instalacji domowej ma opór około 530 Ω. Jakie jest natężenie prądu płynącego przez żarówkę?
(Wynik podaj z dokładnością do 0,01 A).Odpowiedź: 0,43 A.
- umiejętność analizowania schematów obwodów elektrycznych
Przykład:
Wykorzystując akumulator 12 V i żarówkę o oporze 120 Ω uczniowie zbudowali obwód elektryczny według schematu przedstawionego na rysunku: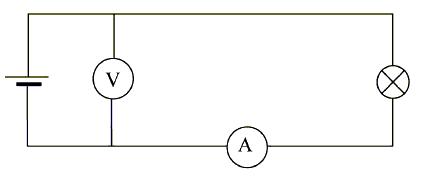
Nazwij trzy pozostałe elementy tego obwodu i określ wskazania mierników.
Odpowiedź: Trzy pozostałe elementy obwodu to: woltomierz, amperomierz i przewody. Wskazanie woltomierza: 12 V, amperomierza: 0,1 A.
- umiejętność obliczania pracy i mocy prądu elektrycznego oraz kosztu zużytej energii elektrycznej
Przykład:
Żarówka o mocy 60 W paliła się w listopadzie codziennie przez 5 godzin. 1 kWh pracy prądu kosztuje 30 groszy. Oblicz, ile złotych należy zapłacić za pobraną energię elektryczną.Odpowiedź: 2 zł 70 gr.
Opracował mgr Krzysztof Zawadzki – nauczyciel Firmy "MARKA"
Sprawdź kursy przygotowawcze w Warszawie – www.marka.edu.pl
Z analizy testów CKE przeprowadzonej przez nauczycieli Firmy „MARKA”, wynika, iż pewne zagadnienia w testach egzaminacyjnych w latach 2002-2012 pojawiały się w częściej niż inne. Wielce prawdopodobne, że i w tym roku można spodziewać się tego typu zadań.
- umiejętność rozpoznawania związków chemicznych (znajomość ich nazw oraz wzorów sumarycznych i strukturalnych)
Przykład:
Podstawowymi składnikami substancji zapachowych wielu roślin są estry. Można je przedstawić wzorem ogólnym: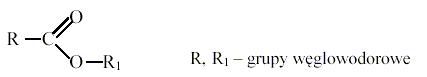
Estrem jest związek o wzorze:

Odpowiedź: D. - znajomość najważniejszych typów reakcji chemicznych
Przykład:
Elementy kolejki wąskotorowej wykonuje się ze stopu, w skład którego wchodzi żelazo. Pierwiastek ten w reakcji z pewnym kwasem tworzy chlorek żelaza (II). Równanie opisujące tę reakcję to:
A. Fe + Cl2 → FeCl2
B. 2 Fe + 3 Cl2 → 2 FeCl3
C. Fe + 2 HCl → FeCl2 + H2 ↑
D. 2 Fe + 6 HCl → 2 FeCl2 +3 H2 ↑Odpowiedź: C.
- znajomość pojęć dotyczących roztworów (nienasyconych i nasyconych) i rozpuszczalności
Przykład:
Wykres przedstawia zależność rozpuszczalności dwutlenku węgla w wodzie od temperatury: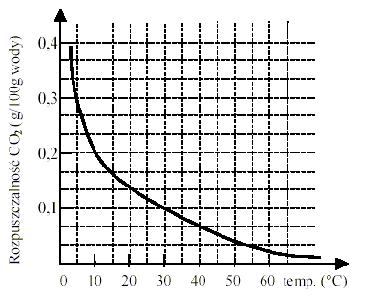
100 g wody o temperaturze 5°C nasycono dwutlenkiem węgla. Ile gramów CO2 wydzieli się w postaci gazu, gdy ten roztwór ogrzejemy do temperatury 30°C?
Odpowiedź: 0,2 g.
- umiejętność stosowania pojęcia stężenia procentowego roztworu
Przykład:
Woda morska zawiera średnio 3,5% soli. Ile wody destylowanej należy dolać do 100 g wody morskiej, aby otrzymać roztwór o stężeniu dwa razy mniejszym?A. 100g
B. 96,5 g
C. 98,25 g
D. 200gOdpowiedź: A.
- znajomość zastosowań związków chemicznych w żywieniu i w życiu codziennym
Przykład:
Nadmierny wzrost stężenia kwasu solnego w żołądku człowieka powoduje chorobę zwaną nadkwasotą. Która z substancji, będąc składnikiem lekarstwa na nadkwasotę, zmniejszałaby stężenie kwasu?A. Chlorek sodu – NaCl.
B. Roztwór kwasu octowego – CH3COOH.
C. Wodorotlenek glinu – Al(OH)3.
D. Roztwór glukozy – C6H12O6.Odpowiedź: C – zajdzie reakcja zobojętniania.
Umiejętność stosowania pojęcia stężenia procentowego roztworu, zastosowania wzoru na stężenie do obliczeń chemicznych.
Woda morska zawiera średnio 3,5% soli.
Zadanie 1. (0–1)
Ile soli zawierają 2 kilogramy wody morskiej?
A.7 g B. 70 g C. 700 g D. 7000 g
Odp.B
Zadanie 2. (0–1)
Z ilu kilogramów wody morskiej otrzymamy 7 kilogramów soli?
A.2 B. 20 C. 200 D. 2000
Odp.C
Zadania z wykorzystaniem umiejętności odczytywania danych z wykresu i ich interpretacja, znajomości zastosowań związków chemicznych w żywieniu i w życiu codziennym, umiejętności posługiwania się skalą kwasowości.
Schemat i tabela do zadań 3 i 4
Skala pH służy do określania odczynu badanej substancji.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| Odczyn kwaśny | Odczyn obojętny | Odczyn zasadowy | |||||||||||
| Roztwór | pH |
|---|---|
| woda sodowa | 5,5 |
| sok pomarańczowy | 3,5 |
| coca-cola | 3,0 |
| mleko | 6,5 |
| woda destylowana | 7,0 |
| amoniak | 11,5 |
| preparat do udrażniania rur | 14,0 |
Zadanie 3. (0–1)
Który z podanych napojów ma najbardziej kwasowy odczyn?
A.Mleko. B. Coca-cola. C. Woda sodowa. D. Sok pomarańczowy.
Odp.B
Zadanie 4. (0–1)
Wybierz zdanie prawdziwe.
A. Woda sodowa ma odczyn zasadowy.
B. Woda destylowana ma odczyn obojętny.
C. Roztwór amoniaku ma odczyn kwasowy.
D. Preparat do udrażniania rur ma właściwości silnego kwasu.
Odp.B
Umiejętność odczytywania danych z układu okresowego i określanie właściwości pierwiastków chemicznych.
Schemat do zadań 5 i 6.
Wzrost aktywności chemicznej można przedstawić w następujący sposób:
| K Na Ca Mg Al Zn Fe Sn Pb H Bi Cu Hg Ag Pt Au |
Metale aktywniejsze od wodoru, wypierające go z zimnej wody i kwasów (reagują z zimną wodą). |
|
Metale aktywniejsze od wodoru, wypierające go z gorącej wody i kwasów (reagują z gorącą wodą i kwasem).
|
|
|
Metale mniej aktywne od wodoru, nie wypierające go z wody i kwasów.
|
Zadanie5. (0-1)
Wybierz zdanie prawdziwe.
A. Sód (Na) reaguje z wodą.
B. W reakcji srebra (Ag) z ZnCl2 wydzieli się cynk (Zn).
C. Złoto (Au) jest bardziej aktywne chemicznie niż potas (K).
D. W reakcji złota (Au) z kwasem siarkowym(VI) wydzieli się wodór.
Odp.A
Zadanie6. (0-1)
Przeprowadzono doświadczenia przedstawione na poniższym rysunku. W której probówce jednym z produktów reakcji jest wodór?
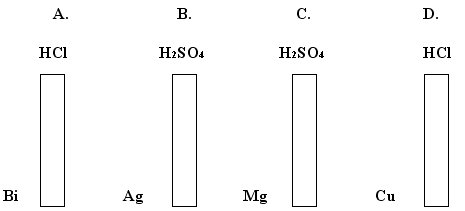
Odp.C
Umiejętność opisywania przedstawionych za pomocą rysunków doświadczeń chemicznych, formułowania spostrzeżeń i wniosków, zapisywania za pomocą równań reakcji chemicznych przedstawionych procesów.
Zadanie 7 (0 – 3)
Tomek wykonał doświadczenie, w którym na cynk podziałał kwasem solnym. Probówkę do zbierania wydzielającego się gazu umieścił w wanience z wodą. Rysunek przedstawia schemat tego doświadczenia.

1. Zapisz równanie reakcji zachodzącej w doświadczeniu.
Odp: Zn + 2HCl—>ZnCl2 + H2
2. Nazwij powstałe produkty reakcji, uzupełniając zdanie:
Odp: Produktami reakcji zachodzącej w doświadczeniu są: chlorek cynku (II) i wodór.
3. Napisz, w jaki sposób zidentyfikujesz wydzielający się gaz.
Odp: Do wylotu probówki z wydzielonym gaz przyłożę zapaloną zapałkę( łuczywo). Usłyszymy wtedy charakterystyczne pyknięcie( odgłos, szczęknięcie itp. określenia)
Umiejętność wskazania zastosowań związków chemicznych i reakcji chemicznych w procesach życiowych i w życiu codziennym ( umiejętność powiązania wiedzy chemicznej z biologiczną i fizyczną).
Zadanie8. (0-1)
Następnego dnia po wycieczce rowerowej uczestnicy odczuwali ból mięśni. Przyczyną tych dolegliwości był nagromadzony w mięśniach kwas mlekowy, powstający w wyniku
A. oddychania tlenowego.
B. oddychania beztlenowego.
C. wymiany gazowej w tkankach.
D. połączenia tlenu z hemoglobiną.
Odp.B
Zadanie 9. (0-1)
Procesy zachodzące w naszym otoczeniu przebiegają z wydzielaniem ciepła do otoczenia (egzotermiczne) lub z pobieraniem ciepła z otoczenia (endotermiczne). Procesem endotermicznym jest
A. prażenie skały wapiennej.
B. spalanie drewna w ognisku.
C. mieszanie wapna palonego z wodą.
D. wlewanie kwasu siarkowego do wody.
Odp.A
Zadanie 10. (0-1)
Podczas gotowania lub smażenia jaja kurzego, białko ścina się nieodwracalnie. Innym czynnikiem powodującym nieodwracalne ścinanie białka jest
A.zimna woda.
B. sól kuchenna.
C. alkohol etylowy.
D. roztwór cukru.
Odp.C
Umiejętność rozpoznawania związków organicznych, znajomość ich wzorów sumarycznych i umiejętność rozpoznawania grup funkcyjnych i klasyfikowania na ich podstawie do odpowiednich grup związków.
Zadanie 11. (0-1)
Marta przygotowała prowiant na wycieczkę rowerową. Pakowane przez nią produkty żywnościowe zawierają ważne dla organizmu związki chemiczne. Które z nich są dlaorganizmu głównie źródłem energii?
A. białka B. cukry C. sole mineralne D. Witaminy
Odp.B
Zadanie 12. (0-1)
Po całodniowej wycieczce rowerowej Marta odczuła ból w mięśniach spowodowany między innymi wytworzeniem się kwasu mlekowego. Związek ten można opisać
wzorem: CH3 CH COOH
OH
Zamieszczona w ramce grupa funkcyjna, charakterystyczna dla kwasów organicznych,nazywa się:
A. węglowodorową B. wodorotlenową C. karboksylową D. estrową
Odp.C
Umiejętność rozpoznawania związków chemicznych, znajomość ich wzorów sumarycznych i umiejętność klasyfikowania ich do odpowiednich grup związków(np. Sole, kwasy, zasady).
Zadanie 13. (0 – 1)
Wskaż zestaw, który zawiera wyłącznie wzory sumaryczne soli.
A.NaCl , MgSO4 , CaCl2 , HNO3
B. NaCl , CaSO4 , CaCl2 , Al(OH)3
C. NaCl, Ca(OH)2 , HCl , Mg3(PO4)2
D. NaCl , KNO3, MgSO4 , CaSO4
Znajomość rozpoznawania najważniejszych typów reakcji chemicznych, umiejętność pisania równań reakcji.
Zadanie 14. (0 – 1)
Wskaż reakcję zobojętniania.
A. 2Na + H2SO4 -> Na2SO4 + H2
B. 2NaOH + H2SO4 -> Na2SO4 + 2H2O
C. Na2O + H2SO4 -> Na 2SO4 + H2O
D. Na2CO3 + H2SO4 -> Na2SO4 + H2CO3
Odp.B
Zadanie 15. (0–2)
Woda gazowana zawiera rozpuszczony w wodzie dwutlenek węgla. Niewielkie ilości tego gazu reagują z wodą, tworząc kwas węglowy.
Napisz równanie reakcji tworzenia się tego kwasu.
Zadanie 16. (0-3)
Na zajęciach kółka chemicznego uczniowie przeprowadzali reakcję zobojętniania. Do roztworu wodorotlenku sodu (MNaOH = 40u) dodali fenoloftaleinę, a następnie wkraplali rozcieńczony roztwór kwasu mrówkowego (MHCOOH = 46u). Punkt zobojętnienia uzyskali w momencie odbarwienia wskaźnika. Zapisz równanie przeprowadzonej reakcji i oblicz, ile gramów kwasu potrzeba do zobojętnienia roztworu zawierającego 10 gramów NaOH.
Równanie.
Obliczenia: 40u 46u
M. NaOH =40u 10g x
M HCOOH=46u 40u/46u =10g/x
x=10g*46u/40u
x =11,5g
Odpowiedź: Do zobojętnienia zasady potrzeba 11,5g kwasu mrówkowego.
Umiejętność czytania ze zrozumieniem, wykonywania obliczeń chemicznych dotyczących obliczania mas cząsteczkowych.
Zadanie 17. (0 – 1)
Na rysunku przedstawiono wybrane informacje z układu okresowego pierwiastków.
(Masy atomowe podane są w zaokrągleniu do jedności).
|
24 Mg 12 magnez
|
75 As 33 arsen |
16 O 8 tlen |
Korzystając z nich, oblicz masę cząsteczkową związku chemicznego o wzorze
sumarycznym Mg3(AsO4)2.
A. 164 u
B. 211 u
C. 350 u
D.130 u
Odp.D
Zadanie 18. (0-2)
Pewien pierwiastek, umownie oznaczony literą E, tworzy tlenek o ogólnym wzorze EO3.
Jaki to pierwiastek, jeżeli masa cząsteczkowa jego tlenku wynosi 80u? Zapisz obliczenia.( Masa atomowa tlenu=16u)
Obliczenia:
mE = mczą – 3mO
mE = 80u – 3* 16u
mE = 32u E = S (siarka)
Odp. Szukanym pierwiastkiem jest siarka ( m=32u).
Umiejętność stosowania pojęcia stężenia procentowego roztworu, zastosowania wzoru na stężenie do obliczeń chemicznych.
Woda morska zawiera średnio 3,5% soli.
Zadanie 19. (0-1)
Ile soli zawierają 2 kilogramy wody morskiej?
A. 7 g B. 70 g C. 700 g D. 7000 g
Odp.C
Zadanie 20. (0-1)
Z ilu kilogramów wody morskiej otrzymamy 7 kilogramów soli?
A.2 B. 20 C. 200 D. 2000
Odp.C
Sprawdź kursy przygotowawcze w Warszawie – www.marka.edu.pl
Z analizy testów CKE przeprowadzonej przez nauczycieli Firmy "MARKA", wynika, iż pewne zagadnienia w testach egzaminacyjnych w latach 2002-2008 pojawiały się w częściej niż inne. Wielce prawdopodobne, że i w tym roku można spodziewać się tego typu tematów tzw. "pewniaków".
Wiedza i umiejętności potrzebne z zakresu:
- Integrowanie wiedzy z różnych działów chemii i innych dziedzin nauki, np. fizyki, matematyki, biologii i geografii – określanie stężeń różnych roztworów (np. woda morska),
- pisanie i wyrównywanie równań reakcji otrzymywania tlenków, wodorotlenków, zasad, kwasów i soli; interpretowanie zapisanych procesów (np. reakcje zobojętniania); znajomość właściwości grup związków; zapisywanie reakcji jonowych zobojętniania na podstawie reakcji cząsteczkowych,
- zapisywanie wzorów sumarycznych, kreskowych substancji (z punktu 2) oraz podawanie nazw chemicznych, a dla niektórych minerałów również nazw zwyczajowych (np. wapień, wapno palone, saletra amonowa),
- opisywanie i uzupełnianie schematów, rysunków i tabel (np. schematów przebiegu doświadczeń metali z kwasem, określenie funkcji przyrządów na rysunku),
- rozwiązywanie zadań rachunkowych z wykorzystaniem wzorów chemicznych, matematycznych, a także fizycznych (np. stężenie procentowe, gęstość),
- wyjaśnianie zależności między budową atomu a położeniem pierwiastka w układzie okresowym pierwiastków, przewidywanie budowy wewnętrznej atomu (liczba powłok i elektronów walencyjnych),
- znajomość podstawowych grup związków organicznych i reakcji ich otrzymywania oraz reakcji charakterystycznych (podstawianie, przyłączanie),
- umiejętność określenia funkcji biologicznych związków organicznych np. alkany, cukry, białka.
Do tej pory na egzaminach pojawiały się pytania dotyczące m.in.
- przebiegu doświadczeń na podstawie przedstawionych schematów,
- formułowanie spostrzeżeń, wniosków, pisanie równań reakcji,
- zadania z wykorzystaniem stężeń procentowych,
- odczytywanie i interpretowanie wielkości z wykresu,
- wzory i nazwy związków organicznych (kwasy, estry).
Opracowała mgr Ewa Kotara-Szopa – nauczycielka w LO im. Herberta
Sprawdź kursy przygotowawcze w Warszawie – www.marka.edu.pl
Z analizy testów CKE przeprowadzonej przez nauczycieli Firmy „MARKA”, wynika, iż pewne zagadnienia w testach egzaminacyjnych w latach 2002-2012 pojawiały się częściej niż inne. Wielce prawdopodobne, że i w tym roku można spodziewać się tego typu zadań.
- integrowania wiedzy z różnych działów biologii i dziedzin nauki np. chemii, geografii i fizyki do wyjaśniania zjawisk biologicznych, szczególnie ekologicznych, np. kwaśnych deszczy, efektu cieplarnianego;
Przykład:
Po biegu maratończyk poczuł silny ból mięśni łydki. Bezpośrednia jego przyczyna to:A. Skrobia
B. Kwas mlekowy
C. Glikogen
D .GlukozaOdpowiedź: B
- podstawowych form ochrony przyrody w Polsce oraz z zakresu krążenia energii i materii w ekosystemie;
Przykład:
Na wysypisko śmieci trafia dużo plastikowych butelek. Naukowcy udowodnili, że z takich butelek można wyprodukować koce lepsze od wełnianych, bo nie wywołujące alergii. Wybierz nazwę procesu umożliwiającego wytwarzanie koców z plastikowych butelek.A. Rekultywacja
B. Segregacja
C. Recycling
D. SelekcjaOdpowiedź: C
- rozpoznawania na rysunku pospolitych gatunków drzew, krzewów, zbóż i chwastów;
Przykład:
Rozpoznaj wyżej podane gatunki zbóż i podpisz ilustracje, wybierając odpowiednią nazwę: kukurydza, pszenica, żyto, owies, jęczmień, proso.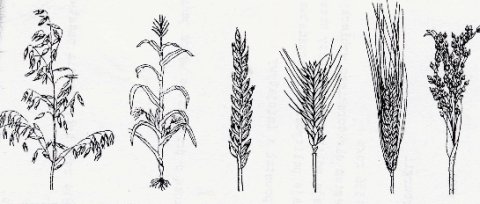
Odpowiedź: owies, kukurydza, pszenica, żyto, jęczmień, proso
- opisywania i uzupełniania schematów i rysunków, np. dotyczących fotosyntezy, odczytywania informacji z tabeli;
Przykład:
Schemat przedstawia reakcję fotosyntezy związków organicznych przy udziale energii słonecznej. Wybierz prawidłowy zapis reakcji fotosyntezy: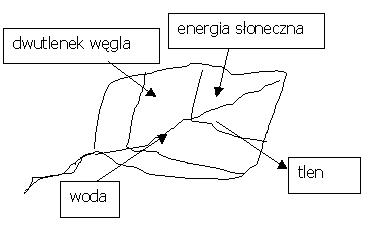
A. 6CO2 + 6H2O → C6H12O6 + 6O2
B. 6CO2 + energia słoneczna → C6H12O6 + 6O2
C. 6H2O + energia słoneczna → C6H12O6 + 6O2
D. 5CO2 + 5H2O → C5H10O5 + 5O2Odpowiedź: A
- wyjaśniania związków między budową i funkcją organów oraz układów wewnętrznych człowieka i roślin;
Przykład:
Które zdanie opisuje związek miedzy budową skórki liścia i funkcją przez nie pełnioną?A. Skórka liścia pokrywa dolną i górną stronę blaszki liściowej
B. Skórka chroni liść przed utratą wodą i wniknięciem niepożądanych substancji oraz drobnoustrojów
C. Komórki skórki mają zgrubiałe ściany komórkowe i nie zawierają chlorofilu
D. Komórki skórki ściśle przylegają do siebie, dzięki czemu chronią liść przed utratą wodyOdpowiedź: D
- podstawowych procesów biochemicznych, np. oddychania i fotosyntezy.
Przykład:
Określ, w której części układu oddechowego człowieka zachodzi proces wymiany gazowej oraz w której strukturze komórkowej odbywają się reakcje oddychania tlenowego.Odpowiedź: Pęcherzyki płucne, cytoplazma i mitochondrium
- Czynności życiowe organizmów
Zadanie 1 /1 punkt/
Fotosynteza to proces, w którym energia świetlna jest wykorzystywana do produkcji cukru w komórkach roślinnych. Zaznacz w odpowiednich miejscach na rysunku nazwy gazów, jakie są wykorzystywane i produkowane podczas tego procesu.
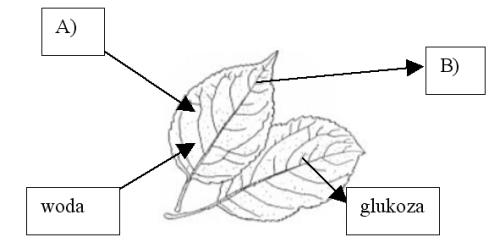
Odpowiedź: A) dwutlenek węgla B) tlen - Ekologia
Zadanie 2 /1 punkt/
W biocenozie pola może funkcjonować następująca sieć pokarmowa:
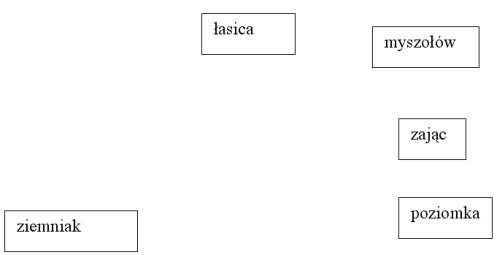
Wypisz z tej sieci pokarmowej wszystkich producentów i podaj ich rolę w tym ekosystemie.Odpowiedź: Producentami są: ziemniak, marchew, poziomka. W tym ekosystemie producenci stanowią pokarm dla konsumentów I rzędu / roślinożerców/.
Inna możliwa odpowiedź: Producenci wydzielają tlen w wyniku fotosyntezy, który jest pobierany do oddychania prze organizmy żyjące na polu.
- Botanika praktyczna
Zadanie 3 /1 punkt/
Warzywa stosowane powszechnie do gotowania zupy nazwano włoszczyzną. Zaznacz prawidłowy skład włoszczyzny:- A. Cebula, marchew, kapusta, rzodkiew
- B. Marchew, seler, szczypior, rzodkiew
- C. Marchew, seler, por, pietruszka
- D. Por, pietruszka, kapusta, burak
Odpowiedź: C)
Zadanie 4 /1 punkt/ Ochrona środowiska
Gdy robimy zakupy, zachowujemy się tak, aby jak najmniej szkodzić środowisku. Zaznacz dwa zachowania niewłaściwe:- A. Wybieram proszek do prania bez fosforanów
- B. Kupuję napoje tylko w butelkach plastikowych
- C. Zakupy ze sklepu przynoszę w koszyku
- D. Kupuję dezodoranty w aerozolu z freonem
Odpowiedź: B), D)
- Botanika praktyczna
Zadanie 5 /1 punkt/
Norka amerykańska sprowadzona do Europy doprowadziła do ograniczenia liczebności rodzimej norki europejskiej. Jest to przykład zależności zwanej:- A. Drapieżnictwa
- B. Konkurencji
- C. Komensalizmu
- D. Pasożytnictwa
Odpowiedź: B
Sprawdź kursy przygotowawcze w Warszawie – www.marka.edu.pl
Z analizy testów CKE przeprowadzonej przez nauczycieli Firmy "MARKA", wynika, iż pewne zagadnienia w testach egzaminacyjnych w latach 2002-2008 pojawiały się w częściej niż inne. Wielce prawdopodobne, że i w tym roku można spodziewać się tego typu tematów tzw. "pewniaków".
Tworzenie własnego tekstu.
Z analizy testów kompetencji opracowanych przez Centralną Komisję Egzaminacyjną wynika, że najbardziej popularną ze wszystkich obowiązujących form stylistycznych jest rozprawka (pojawiła się do tej pory właściwie na każdym teście próbnym, była formą obowiązujacą na egzaminie gimnazjalnym).
W roku ubiegłym uczniowie mieli za zadanie napisać charakterystykę, zawierała ona jednak elementy typowe dla rozprawki (argumentacja). Należy się spodziewać, że w związku z obowiązującymi standardami wymagań egzaminacyjnych pojawić się mogą (i powinny) inne formy: opis, opowiadanie, artykuł, pamiętnik, recenzja, przemówienie, wywiad. Od uczniów wymaga się również, by budowali poprawne pod względem jezykowym i stylistycznym wypowiedzi takie jak: notatka, ogłoszenie, zaproszenie, dedykacja, podanie, życiorys, list. Formy te wymagają utrzymania pewnego schematu, porządku, a realizacja poszczególnych ich elementów punktowana jest dość rygorystycznie.
Należałoby zwrócić uwagę na ćwiczenia, w czasie których dokonywane są celowe operacje na tekście – streszczanie, rozwijanie, przekształcanie stylistyczne (np. zmiana formy narracji, uzupełnianie fragmentu tekstu opisem lub dialogiem bohaterów utrzymanym w konwencji utworu).
- Rozprawka – ta forma wypowiedzi pojawiła sie na egzaminie gimnazjalnym trzykrotnie
2002 r. – Warto poznawać dorobek naszych przodków. Napisz rozprawkę, w której ustosunkujesz sie do tej opinii. Odwołaj się do trzech przykładów osiągnięć cywilizacyjnych (jednego z arkusza i dwóch własnych).
2003 r. – Napisz charakterystykę wybranej postaci literackiej, dowodząc, że warto ją ukazać w teatrze lub filmie. W temacie pracy mowa jest wprawdzie o charakterystyce, jednakże stosowanie argumentacji jest typowe dla rozprawki.
2004 r. – Napisz rozprawkę na temat: Jeśli "nie szata zdobi człowieka", to w czym tkwi jego wartość. W pracy posłuż sie przykładami z literatury, historii bądź sztuki.
- Notatka
2002 r. – Napisz notatkę do kroniki szkolnej zawierajacą informacje o przebiegu wycieczki do muzeum sztuki starożytnej. Uwzględnij także swoje wrażenia z pobytu w tym muzeum. Praca ta ma charakter sprawozdania z wycieczki (w formie notatki) , ktrórego ważnym elementem jest ocena wydarzenia.
- Hasło słownikowe
2002 r. – Napisz tekst, który zostałby zamieszczony w encyklopedii jako objaśnienie hasła "archeologia".
- Podanie
2003 r. – Napisz podanie do dyrektora teatru zawierające prośbę o wypożyczenie kostiumów dla aktorów grajacych w szkolnym przedstawieniu "Antygony". Wymień trzy postacie z tragedii Sofoklesa, dla których będą one potrzebne. Należało uwzględnić wszystkie elementy składowe charakterystyczne dla tej formy wypowiedzi.
- Zaproszenie
2004 r. – Zredaguj zaproszenie na otwarcie wystawy pt. Historia mody. Posłuż się fikcyjnymi danymi.
Lektury
Pytania egzaminacyjne dotyczyły zamieszczonych w teście fragmentów Faraona, Antygony i Pana Tadeusza, wymagały jednak od zdającego pewnej wiedzy historycznej i orientacji w epokach (starożytność, oświecenie, romantyzm).
Czytanie i odbiór tekstów kultury.
Od ucznia trzeciej klasy gimnazjum wymaga się, by potrafił trafnie interpretować teksty kultury (młodzież często ma trudności nawet ze zdefiniowaniem tego pojęcia), odróżniał fakty od opinii, prawdę historyczną od fikcji, dostrzegał związki danego tekstu z historią, tradycją, filozofią i umiał odnieść je do współczesności.
W testach egzaminacyjnych (2002-2004) odwoływano się do sztuki egipskiej, greckiej i rzymskiej, poszukiwano starożytnych źródeł współczesnej architektury czy też mody.
W tekstach kultury gimnazjalista powinien dostrzegać typowe środki wyrazu , wyjaśnić, w jakim celu zostały użyte, określić ich funkcje. Dużą trudność sprawić może odnalezienie i nazwanie środków stylistycznych w tekście literackim, przytoczenie odpowiedniego fragmentu z użyciem odpowiednich znaków interpunkcyjnych.
- Środki stylistyczne
2002 r. – należało wskazać środki stylistyczne dominujące w podanym fragmencie tekstu (powtórzenia, wyliczenia, apostrofy, pytania retoryczne)., a także (kolejne polecenie) wypisać z materiału źródłowego jedną ze znajdujacej sie w nim przenośni.
2003r. – należało wypisać i nazwać jeden ze środków poetyckich tworzących nastrój we fragmencie zacytowanego wiersza.
2004 r. – zadaniem gimnazjalisty było nazwanie zastosowanego w wypowiedzeniu Moda jest tyran środka stylistycznego; należało go wybrać spośród podanych (epitet, kontrast, apostrofa, przenośnia).
Kolejnym ważnym elementem jest umiejętność odczytywania różnorodnych tekstów na poziomie dosłownym i przenośnym. O ile z tym pierwszym młodzież radzi sobie dość sprawnie, o tyle zrozumienie i nazwanie ukrytego, symbolicznego sensu sprawia jej trudności.
Kształcenie językowe.
W dotychczasowych testach nie pojawiły sie wprawdzie pytania odwołujące się do teoretycznej wiedzy gramatycznej, niemniej jednak pewne kwestie (podmiot, imiesłowowy równoważnik zdania i związana z tym interpunkcja, części mowy, budowa słowotwórcza wyrazu) należało roztrzygnąć, udzielając prawidłowych odpowiedzi w pytaniach zamkniętych.
- Gramatyka – słowotwórstwo
W dotychczasowych testach pojawiły sie pytania ze słowotwórstwa:
2002 r. – Wyrazem o innej budowie słowotwórczej niż pozostałe jest:
- grafolog,
- archeolog,
- kulturoznawca,
- historyk.
2004 r. – Wyraz zetempowski został utworzony z pierwszych liter wyrazów wchodzących w sklad nazwy:
- Związek Młodzieży Polskiej,
- Związek Młodziezy Wiejskiej,
- Zwiazek Harcerstwa Polskiego,
- Zwiazek Młodzieży Socjalistycznej.
- Gramatyka – składnia i leksyka
2003 r. – pytanie dotyczyło funkcji, jaką pełnią w podanym tekście równoważniki zdań (należało wyjaśnić, czy dzięki zastosowaniu równoważników zdań odnośny fragment tekstu stał się unaukowiony, ironiczny, krótszy czy zabawny).
2004 r. – zdanie Prasa donosi, że ostatnim krzykiem mody jest litreatura fantastycznonaukowa należało przekształcić tak, aby własnymi słowami oddać znaczenie wyrażenia ostatni krzyk mody.
W jednym z pytań pojawiły się również terminy gramatyczne z fleksji i składni, ale samo zadanie dotyczyło narracji.
{mospagebreak title=z 2006&heading= z 2005}
PEWNIAKI AUTORSKIE CZYLI DOKTOR MARCIN
POD-POWIADA:

Po pierwsze spokojnie i radośnie bo egzamin gimnazjalny w swojej humanistycznej odsłonie jest nadzwyczajnie prosty (niektórzy z pewną racja mówią, że prostacki)
Podaję Wam tu tylko informacje przydatne dla wszystkich, którzy zmierzą się za kilka miesięcy z gimnazjalnym „wykończeniem" szkoły.
Jeżeli ktoś zapragnie konkretnych, bardzo szczegółowych informacji. (np. o tytułach podręczników, albo: gdzie znaleźć najpewniejsze info na dany temat albo: tematy prac albo: jakie są tajemnice poszczególnych form wypowiedzi pisemnej … albo … zapraszam do pytania poprzez maila: migdalowa.brama@neostrada.pl albo:marlowmartin@poczta.onet.pl
Do rzeczy zatem:
TEST…TEST…CZEKA CIĘ ZMAGANIE Z TESTEM. A TEST JEST ZAWSZE TAK PROSTY, ŻE AŻ ZĘBY ZGRZYTAJĄ, KIEDY WIDZI SIĘ W TEŚCIE BŁĘDNE ODPOWIEDZI. TEST JAK U BRACI AMERYKANÓW JEST TESTEM UMIEJĘTNOŚCI. TEST ZACZYNAJ ROZWIĄZYWAĆ KONIECZNIE UWZGLĘDNIAJĄC DWA PONIŻSZE PEWNIAKI TESTOWE (jednak pamiętaj ! Nic nie zastąpi rozwiązania ‘na czas’ co najmniej 10 TESTÓW ):
Nie jest stratą czasu ale zyskiwaniem punktów pobieżne przejrzenie całego testu (ok.10min.). Nasze mózgownice rozpracowują później wiele zadań jednocześnie, kiedy koncentrujemy się na poszczególnych pytaniach.
test zawsze ma swoją „główną tajemnicę" (szczegółowe pytania na ten temat kierujcie do mnie poprzez maila), zasadę, która odkryta pozwoli szybciej i skuteczniej pracować (do takich ‘tajemnic’ należy np. sposób eliminowania dwóch spośród czterech odpowiedzi, a z pozostałymi dwiema co najmniej 2 razy łatwiej sobie poradzisz. Rozwiązujemy zawsze „od początku do końca" nie tracąc czasu w tych miejscach, gdzie nie wiemy, następnie piszemy wypracowanie, a jeżeli czas pozwoli (tak jakby miał on coś do gadania) wracamy do pytań nierozwiązanych,
(!!!) PISANIE
WYPRACOWANIE I FORMA KRÓTKA:
PEWNIAK NUMER1: nie wolno zapominać, że za pis-anie można ‘złapać’ niemal połowę z 50 możliwych punktów ( tu traci się najwięcej niestety !)
PEWNIAK NUMER2: JEŻELI NIE ZNASZ ZASAD PISANIA PODANYCH NIŻEJ FORM TO PUNKT TWOJEGO STARTU JEST SŁABY (NIE JEST TO PULL POSITION).
Musisz orientować się w sposobie komponowania następujących form (te podane tłustym drukiem są również 'tłuste’ w punkty):rozprawka…recenzja…reportaż…list (i jego odmiany)…opowiadanie…notatka…charakterystyka…opis (i jego rodzaje) … streszczenie … podanie … sprawozdanie … protokół … telegram … zaproszenie … przemówienie …wywiad … ogłoszenie …… instrukcja obsługi … przepis (i jako ważny dodatek:sztuka interpretowania wiersza i zasady cytowania).
PEWNIAK NUMER 3: jeżeli po zapoznaniu się z nazwami znasz już stan Swojej wiedzy/ niewiedzy zadecyduj, do której z poniższych kategorii się zaliczasz: 1. SŁABY 2. ŚREDNI 3. DOBRY
POWINIENEŚ ZROBIĆ, CO NASTĘPUJE:
słaby…nie umiesz i nie lubisz pisać: koniecznie poznaj zasady rządzące poszczególnymi formami wypracowań (kurs, korek lub wysiłek własny). Żadna forma nie powinna być dla Ciebie’ białą plamą" dlatego niezbędne wydaje się napisanie min 2 razy każdej formy
średni … ‘raczej’ umiesz i raczej nie lubisz pisać: znajdź prace innych; takie świetnie napisane i analizuj je. Sam koniecznie napisz te, w których nie czujesz się pewnie.
dobry …potrafisz pisać i lubisz lub nie lubisz pisać: powinieneś solidnie skontaktować się z najlepszymi pracami Twoich rówieśników i ‘rozegrać wirtualnie, w głowie’ wybrane na „chybił- trafił" tematy wypracowań.
PEWNIAK NUMER 4: niezbędne dodatki: przejrzyj programy nauczania (to na nich oparte są tematy, testy i reszta egzaminacyjnych gier)…obejrzyj film, idź do teatru i czytaj gazety ok. 2 tygodnie przed próbą egzaminacyjną, wybierz ulubieńca spoza lektur szkolnych…napisz "ćwiczebnie" min. 7 testów włącznie z wypracowaniami pilnując objętości prac i czasu.
MEGAPEWNIAK NUMER 6: BĘDZIE ZREALIZOWANY MNIEJ WIĘCEJ W POŁOWIE MARCA: Piszący te słowa jak dotąd ZAWSZE (!!) ‘odgadywał’ tematy wypracowań egzaminacyjnych (nie w dosłownym brzmieniu ale jeśli idzie o treść zawsze w 10).
Kiedy już moja intuicja zadziała podam tematy w tym miejscu, a Ty koniecznie prze- MYŚL i na-PISZ ‘jakby co: niemal gotowiec w głowie.
Na razie pozdrawiam. Do następnego zekranizowania
marcin jędrzejczak

PEWNIAKI NIE MOGĄ BYĆ TAKIE PEWNE (WTEDY JEST TO LANSERSTWO I TUPET) PEWNIAKI MAJĄ BYĆ …PRAKTYCZNE
Pewna jest tylko śmierć. Tak mawiają. Na początek nie zgódźmy się z tym. Pewne jest, że megaobowiązkowe formy pisania dla kończącego gimnazjum to: 1. OPISY (przeżyć wewnętrznych, krajobrazu/przestrzeni, przedmiotu), 2. OPOWIADANIA (realistyczne, fantastyczne, z narratorem wszechwiedzącym i/lub subiektywnym/pierwszoosobowym),3. LISTY(prywatny, oficjalny, otwarty), 4. notatki(plan ramowy, plan szczegółowy, tabela, wykres, cytat, opis/np.bibliograficzny, konspekt), 5.podanie i życiorys, 6. reportaż, 7. recenzje, 8. przemówinie,9. felieton, 10. streszczenie, 11. rozprawka, 12wywiad, 13. sprawozdanie.
Ha? Jest to pewne?! JEST.
Formy’ wytłuszczone SA szczególnie ważne i nikt nie powinien pozwolić sobie na- przetrenować, hmmm czasu mało- N I E Z N A J O M O Ś Ć zasad ich pisania/ komponowania
UWAGA ! UWAGA!!! J)
PRZYSZŁA PORA NA INTUICJĘ MARCINOWĄ:
1 NA FORUM WISI INFORMACJA (PRZYSZŁA DO MNIE – DLA Was o 3-ej parę dni temu. To niemal PRZEDSWIT (ależ piękne słowo!)
Oto Wasz tegoroczny temat (Moi drodzy! Nie mam żadnych ‘wejść’ do autorów testów, tematów itd.)
(Jeżeli intuicja tym razem zawiedzie: wtedy nie bijcie tylko wybaczcie); moja intuicja nie zwalnia Was od posiadania umiejętności napisania głównych form/ wypracowań obowiązujących w programach…
TEMAT: Trzeźwe(racjonalne, materialne?) myślenie czy idealizm? Która postawa wobec życia wydaje się w obecnych czasach bardziej właściwa? Napisz pracę, w której odniesiesz się do treści wiersza…(tu: wiersz ale jaki? Intuicja milczyL)
Zatem:
1. Wyszukajcie (pośród różnych tekstów kultury; książki, spektakle, muzyka życie codzienne przykłady postaw racjonalistycznych i idealistycznych
2. Amerykańcy w waszym wieku Pisza niemal same eseje…u nas esej nie przynależy do ścisłego programu ale refleksje, wypracowanie to właśnie nic innego tylko esej. SIĘGNIJCIE DO ZASAD JEGO KOMPONOWANIA!
3. Dziś- w ciągu dnia- intuicja odezwała się znowu: wygląda na to, że w ramach testu krótką forma będzie
S T R E S Z C Z E N I E ( 3-4- 5 punktów!)
4. Jest taki symbol (nazywa się ‘monogramgwiaxdzisty’)…nie mogę go narysować…pionowa kreska i na niej: x, z ramionami krótszymi niż pionowa kreska. Narysujcie go (ołówkiem!) na kartkach testu albo długopisemJ na reku i co kilka minut popatrzcie przez chwilke na Niego: KONCENTRACJA GWARANTOWANA.
Niech moc będzie z Wami!⅞
Sprawdź kursy przygotowawcze w Warszawie – www.marka.edu.pl
Siedem podstawowych umiejętności egzaminacyjnych
Analiza testów CKE z lat 2002-2012 przeprowadzonej przez nauczycieli Firmy Edukacyjnej Marka wynika nie tylko powtarzalność pewnych zagadnień , ale także kluczowe znaczenie pewnych umiejętności, bez których gimnazjalista nie ma co marzyć o sukcesie na egzaminach z poszczególnych przedmiotów. Jeżeli nie wiecie od czego zacząć swoją powtórkę, to idźcie drogą wskazaną przez autora tego opracowania, p.Krzysztofa Zawadzkiego – nauczyciela Firmy Edukacyjnej Marka, który od ponad 20 lat przygotowuje do egzaminów. Powodzenia!
I umiejętność: odczytywanie informacji przedstawionych w różnej formie (mapy, tabeli, wykresu, rysunku, schematu, fotografii, tekstu)
Przykład 1 – odczytanie informacji z mapy
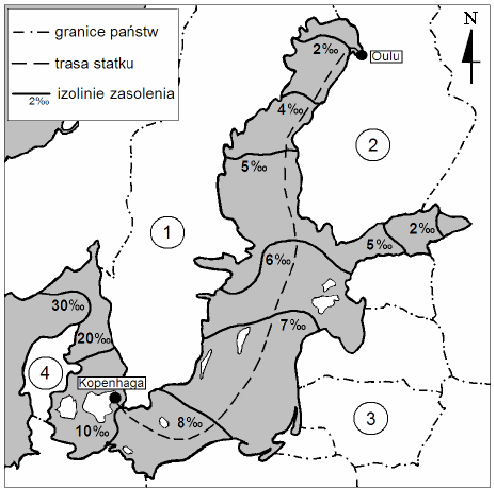
Zasolenie morza określa się jako ilość gramów soli rozpuszczonych w jednym kilogramie wody morskiej i podaje w promilach (‰). Przeciętnie w jednym kilogramie wody morskiej znajduje się 34,5 g różnych rozpuszczonych w niej soli (czyli przeciętne zasolenie wody morskiej jest równe 34,5‰).
Zasolenie Bałtyku (średnio 7,8‰) jest znacznie mniejsze od zasolenia oceanów, co tłumaczy się wielkością zlewiska (duży dopływ wód rzecznych), warunkami klimatycznymi (małe parowanie) oraz utrudnioną wymianą wód z oceanem.
|
Zasolenie Morza Bałtyckiego |
|
|
Na podstawie: J. Kondracki, Geografia fizyczna Polski, Warszawa 1988
Zasolenie zmieniające się od 2‰ do ponad 20‰ mają wody wzdłuż wybrzeża państwa, które na rysunku oznaczono liczbą
A. 1
B. 2
C. 3
D. 4
Przykład 2 – odczytanie informacji z diagramu kołowego
Poważnym problemem są zanieczyszczenia Bałtyku substancjami biogennymi. Diagramy przedstawiają procentowy udział państw nadbałtyckich w zanieczyszczeniu Morza Bałtyckiego związkami azotu (diagram a) i związkami fosforu (diagram b) w 1995 roku.
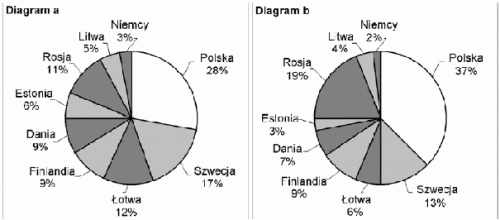
Na podstawie: www.naszbaltyk.pl
Procentowy udział Polski w zanieczyszczeniu Bałtyku związkami azotu w 1995 r. był taki, jak łącznie krajów
A. Szwecji i Rosji
B. Rosji i Łotwy
C. Danii i Finlandii
D. Rosji i Finlandii.
Przykład 3 – odczytanie informacji z wykresu
Na wykresach przedstawiono zależność rozpuszczalności wybranych substancji w wodzie od temperatury.
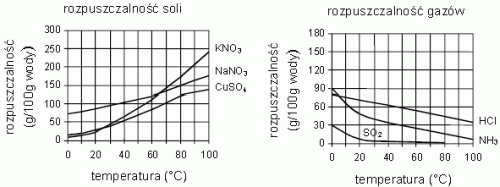
Na podstawie: W. Mizerski, Tablice chemiczne, Warszawa 2003
Korzystając z wykresów, uzupełnij zdania:
Ze wzrostem temperatury rozpuszczalność soli ………………………….. (rośnie / maleje), a gazów ………………………….. (rośnie / maleje). W 100 g wody o temperaturze 500C można rozpuścić co najwyżej ……………………… g NH3.
Przykład 4 – odczytanie informacji z tablicy
Filip zamieścił na swojej stronie internetowej następujące informacje dotyczące planet Układu Słonecznego:
|
Lp. |
Nazwa planety |
Masa planety w stosunku do masy Ziemi |
Liczba księżyców |
|
1. |
Merkury |
0,06 |
0 |
|
2. |
Wenus |
0,82 |
0 |
|
3. |
Ziemia |
1 |
1 |
|
4. |
Mars |
0,11 |
2 |
|
5. |
Jowisz |
317,9 |
16 |
|
6. |
Saturn |
95,18 |
20 |
|
7. |
Uran |
14,5 |
17 |
|
8. |
Neptun |
17,24 |
8 |
|
9. |
Pluton |
0,002 |
1 |
Tablice geograficzne, Wyd. Adamantan, Warszawa 1998
Która z planet o masie mniejszej niż masa Ziemi ma najwięcej księżyców?
A. Mars
B. Saturn
C. Neptun
D. Pluton.
Przykład 5 – odczytanie informacji z diagramu słupkowego
Uczniowie klas trzecich pewnego gimnazjum urządzili w swoich salach wystawy przedstawiające najciekawsze miejsca w różnych krajach. Po obejrzeniu wszystkich ekspozycji przeprowadzona została ankieta, w której uczniowie odpowiadali na pytanie, który kraj chcieliby odwiedzić. Każdy z ankietowanych mógł wybrać tylko jeden kraj.
Oto jakich wyborów dokonali uczniowie.
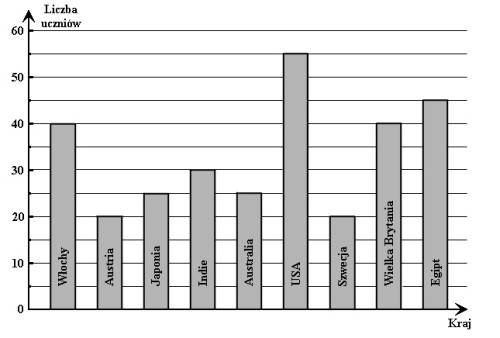
Ilu uczniów uczestniczyło w ankiecie?
A. 310
B. 300
C. 290
D. 250.
II umiejętność: operowanie informacjami (ich selekcja, analizowanie, przetwarzanie, interpretowanie, wykorzystywanie w praktyce)
Przykład 6 – przetworzenie informacji zawartych w tabeli
Tabela przedstawia ceny kart wstępu na pływalnię. Czas pływania uwzględnia liczbę wejść oraz czas jednego pobytu na basenie.
|
Numer karty |
I |
II |
III |
IV |
|
Czas pływania |
10 x 1 godz. |
8 x 1,5 godz. |
20 x 1 godz. |
15 x 1 godz. |
|
Cena karty |
50 zł |
50 zł |
80 zł |
70 zł |
Godzina pływania jest najtańsza przy zakupie karty:
A. I
B. II
C. III
D. IV.
Przykład 7 – przetworzenie informacji zawartych na rysunku
Na podstawie poniższego rysunku wyznacz objętość kamienia wrzuconego do wody:
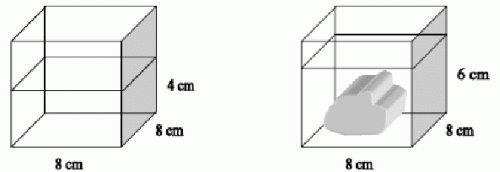
A. 256 cm3
B. 128 cm3
C. 384 cm3
D. 488 cm3.
Przykład 8 – przetworzenie informacji zawartych na wykresie
Wykres przedstawia zależność rozpuszczalności dwutlenku węgla w wodzie od temperatury.
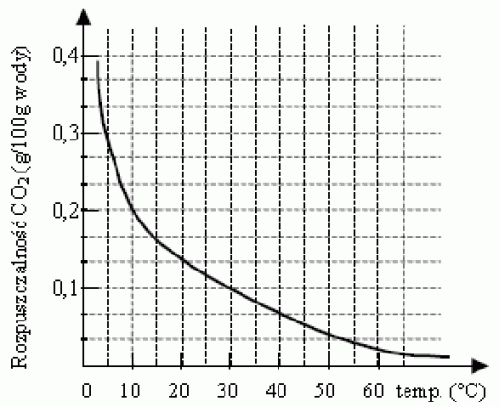
100 g wody o temperaturze 50C nasycono dwutlenkiem węgla. Ile gramów CO2 wydzieli się w postaci gazu, gdy ten roztwór ogrzejemy do temperatury 300C?
A. 0,1
B. 0,2
C. 0,3
D. 0,4.
Przykład 9 – przetworzenie informacji zawartych na mapie
Na mapie zaznaczono 10 krajów, które przystąpiły do Unii Europejskiej 1 maja 2004 roku. Ich powierzchnię podano w tys. km2.
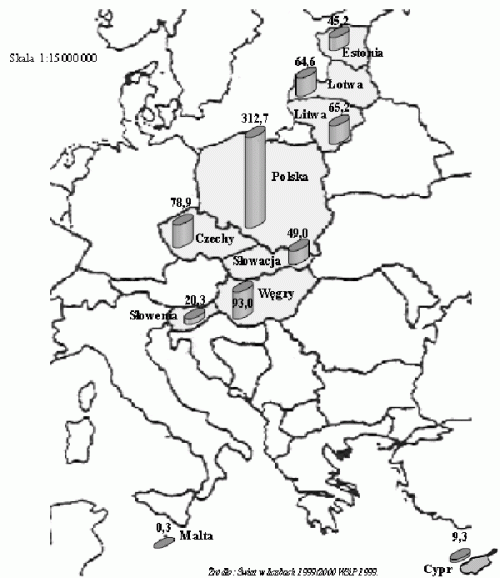
Powierzchnia najmniejszego z tych państw jest mniejsza od powierzchni największego państwa około
A. 15 razy
B. 1042 razy
C. 30 razy
D. 6 razy.
Przykład 10 – przetworzenie informacji zawartych na diagramach
W Londynie ogromnym problemem jest smog, składający się między innymi z tlenków siarki i tlenków azotu. Pewnego dnia w atmosferze znalazła się taka sama masa tlenków siarki co tlenków azotu. Diagramy przedstawiają źródła zanieczyszczeń powietrza tymi tlenkami.
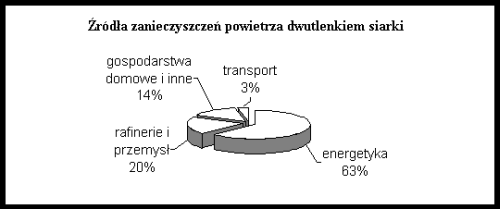

Największa łączna masa wyemitowanych tlenków azotu i tlenków siarki pochodziła z
A. transportu
B. gospodarstw domowych
C. energetyki
D. przemysłu (w tym rafinerii).
Przykład 11 – przetworzenie informacji zawartych w tekście
Biedronki siedmiokropki polują na mszyce w ogrodach i na polach. Mszyce zabezpieczają się przed nimi, wydzielając obronną ciecz, same natomiast żywią się sokiem wyssanym z roślin. Aby ochronić się przed mszycami, rośliny wytwarzają kolce i parzące włoski, które nie zawsze jednak są dostatecznym zabezpieczeniem.
W jaki sposób konsumenci I rzędu, o których mowa w powyższej informacji, bronią się przed naturalnymi wrogami?
Odpowiedź: …………………………………………………………………………………………………….
III umiejętność: wykonywanie obliczeń w sytuacjach praktycznych
Przykład 12 – wykonanie obliczeń na liczbach dziesiętnych
(zadanie z egzaminu gimnazjalnego przeprowadzonego przez CKE w kwietniu 2005 r.)
Montaż instalacji gazowej w samochodzie kosztuje 2208 zł. Samochód spala średnio 7 litrów benzyny lub 8 litrów gazu na każde 100 km drogi. Oblicz, po ilu miesiącach zwrócą się koszty instalacji, jeśli w ciągu miesiąca samochód przejeżdża średnio 2000 km. Zapisz obliczenia.
| cena benzyny | cena gazu |
|---|---|
| 3,80 zł/l | 1,60 zł/l |
Przykład 13 – operowanie procentami
Uzupełnij rachunek wystawiony przez firmę budowlaną, wpisując w wykropkowanych miejscach obliczone wartości:
|
|
Liczba sztuk |
Cena netto |
VAT (22% ceny netto) |
Razem |
|
Okno |
1 |
1200 zł |
………………….. |
……………. |
|
Drzwi |
1 |
………………. |
………………. |
3538 zł |
Przykład 14 – posługiwanie się jednostkami miar i przybliżeniami
Rysunki przedstawiają wskazania wodomierza w dniach 1 września i 1 października.
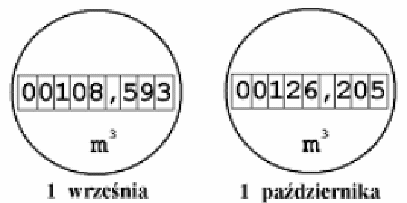
Oblicz, zaokrąglając do całości, ile metrów sześciennych wody zużyto od 1 września do 1 października.
A. 16 m3
B. 17 m3
C. 18 m3
D. 22 m3.
Przykład 15 – posługiwanie się jednostkami miary
Plan kortu tenisowego wykonany w skali 1 : 2000 ma powierzchnię 1 cm2. Jaka jest rzeczywista powierzchnia tego kortu?
A. 2000 m2
B. 20 m2
C. 400 m2
D. 4000 m2.
Przykład 16 – stosowanie własności działań w praktyce
Uczniowie wraz z opiekunami pojechali na wycieczkę do Brukseli. Zwiedzanie Brukseli (520N, 40E) zakończyło się o godzinie 18.00 czasu słonecznego. Która godzina czasu słonecznego była wówczas w Warszawie (520N, 210E)? Zapisz obliczenia.
Przykład 17 – posługiwanie się proporcjami do obliczenia ilości składników mieszaniny
Aby przygotować suchą zaprawę do tynkowania ścian, należy zmieszać piasek, wapno i cement odpowiednio w stosunku 15 : 4 : 1. W którym wierszu tabeli podane są właściwe ilości składników potrzebnych do otrzymania 140 kg takiej zaprawy?
|
|
Piasek (kg) |
Wapno (kg) |
Cement (kg) |
|
I |
101 |
32 |
8 |
|
II |
109 |
24 |
7 |
|
III |
105 |
28 |
7 |
|
IV |
105 |
56 |
14 |
A. I
B. II
C. III
D. IV.
Przykład 18 – obliczanie średniej arytmetycznej liczb
Przez 3 godziny Jacek z Magdą obserwowali ruch samochodowy na moście. Liczyli przejeżdżające pojazdy. Wyniki zapisali w tabeli.
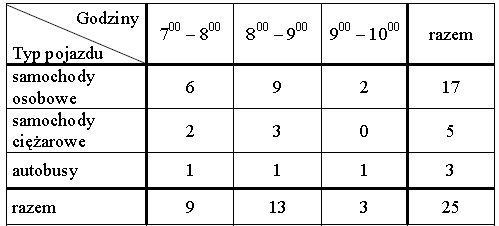
Ile samochodów osobowych przejeżdżało średnio przez most w ciągu jednej godziny obserwacji?
A. ![]()
B. 6
C. ![]()
D. 7.
Przykład 19 – obliczanie kosztu zużytej energii elektrycznej
W ciągu 30 dni w czajniku o mocy 1600 W podgrzewano wodę średnio przez 15 minut dziennie. Oblicz koszt energii elektrycznej zużytej przez czajnik w ciągu tych 30 dni. Przyjmij, że cena 1 kWh energii wynosi 32 gr. Zapisz obliczenia.
IV umiejętność: posługiwanie się własnościami figur
Przykład 20 – zauważanie symetrii figur geometrycznych

Przedstawiona na rysunku flaga Wielkiej Brytanii
A. ma cztery osie symetrii i środek symetrii.
B. ma cztery osie symetrii i nie ma środka symetrii.
C. ma dwie osie symetrii i środek symetrii.
D. ma dwie osie symetrii i nie ma środka symetrii.
Przykład 21 – obliczanie obwodów figur płaskich
Rowerzysta policzył, że podczas jazdy z domu do szkoły koło jego roweru o średnicy 64 cm wykonało 250 obrotów. Przybliżona odległość z domu do szkoły wynosi (![]() 3)
3)
A. 480 m
B. 960 m
C. 7680 m
D. 30720 m.
Przykład 22 – obliczanie pól powierzchni figur płaskich
Przekrój poprzeczny ziemnego wału przeciwpowodziowego ma mieć kształt równoramiennego trapezu o podstawach długości 6 m i 16 m oraz wysokości 12 m. Trzeba jednak usypać wyższy wał, bo przez dwa lata ziemia osiądzie i wysokość wału zmniejszy się o 20% (szerokość wału u podnóża i na szczycie nie zmienia się).
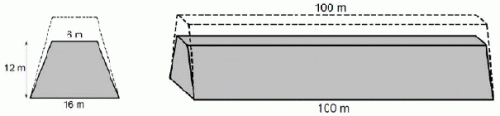
Po zakończeniu osiadania ziemi, w celu zmniejszenia przesiąkania, na zboczu wału od strony wody zostanie ułożona warstwa gliny. Oblicz pole powierzchni, którą trzeba będzie wyłożyć gliną na 100-metrowym odcinku tego wału (wał ma kształt graniastosłupa prostego). Zapisz obliczenia. Wynik podaj z jednostką.

Przykład 23 – obliczanie pól powierzchni brył
Na dziedzińcu przed Luwrem zbudowano szklaną piramidę. Piramida ta ma kształt ostrosłupa prawidłowego czworokątnego o wysokości około 20 metrów i krawędzi podstawy 30 metrów. Wykonaj rysunek pomocniczy wraz z oznaczeniami i oblicz powierzchnię ścian bocznych szklanej piramidy. Zapisz obliczenia.
Przykład 24 – obliczanie objętości brył
Objętość beczki oblicza się wg wzoru: ![]() , gdzie
, gdzie ![]() średnica w miejscu najszerszym,
średnica w miejscu najszerszym, ![]() średnica dna,
średnica dna, ![]() wysokość beczki.
wysokość beczki.
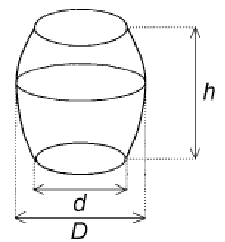
Wojtek obmierzył beczkę w ogrodzie. Ma ona wysokość 12 dm i średnicę dna równą 7 dm. Z powodu trudności ze zmierzeniem średnicy w najszerszym miejscu Wojtek zmierzył obwód w najszerszym miejscu. Jest on równy 33 dm. Oblicz objętość beczki. Dla ułatwienia obliczeń przyjmij ![]() . Zapisz obliczenia.
. Zapisz obliczenia.
V umiejętność: posługiwanie się językiem symboli i wyrażeń algebraicznych (zapisywanie wielkości za pomocą wyrażeń algebraicznych, przekształcanie wyrażeń algebraicznych, zapisywanie związków między wielkościami za pomocą równań)
Przykład 25 – zapisywanie wyrażeń algebraicznych
W wiadrze jest ![]() litrów wody, a w garnku
litrów wody, a w garnku ![]() litrów wody. Ile litrów wody będzie w wiadrze, a ile w garnku, jeśli:
litrów wody. Ile litrów wody będzie w wiadrze, a ile w garnku, jeśli:
1. z wiadra przelejemy do garnka 1,5 litra wody;
2. przelejemy połowę wody z garnka do wiadra?
Wpisz do tabeli odpowiednie wyrażenia algebraiczne.

Przykład 26 – przekształcanie wyrażeń algebraicznych
Objętość (![]() ) cieczy przepływającej przez rurę o polu przekroju
) cieczy przepływającej przez rurę o polu przekroju ![]() oblicza się według wzoru
oblicza się według wzoru ![]() , gdzie
, gdzie ![]() oznacza prędkość przepływu cieczy,
oznacza prędkość przepływu cieczy, ![]() czas przepływu. Który wzór na prędkość cieczy przepływającej przez rurę jest rezultatem poprawnego przekształcenia podanego wzoru?
czas przepływu. Który wzór na prędkość cieczy przepływającej przez rurę jest rezultatem poprawnego przekształcenia podanego wzoru?
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Przykład 27 – układanie równań lub układów równań
Trzy lata temu posadzono przed domem krzew. Co roku podwajał on swoją wysokość i teraz ma 144 cm. Jeśli przez ![]() oznaczymy wysokość krzewu w dniu posadzenia, to informacjom z zadania odpowiada równanie:
oznaczymy wysokość krzewu w dniu posadzenia, to informacjom z zadania odpowiada równanie:
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Przykład 28 – ułożenie i rozwiązanie równania lub układu równań („zadanie tekstowe”)
Na wycieczkę do Brukseli pojechało 38 uczniów i 4 opiekunów. Zarezerwowano dla nich nocleg w pokojach dwu i trzyosobowych. Cała grupa nocowała w 17 pokojach. Wszystkie zarezerwowane pokoje były w pełni wykorzystane. Ile zarezerwowano pokoi dwuosobowych, a ile trzyosobowych? Zapisz obliczenia.
Przykład 29 – analizowanie podanych funkcji
Obserwując zużycie benzyny w swoim samochodzie pan Nowak stwierdził, że jeśli wystartuje z pełnym bakiem i będzie jechał po autostradzie ze stałą prędkością, to zależność liczby litrów benzyny w baku (![]() ) od liczby przejechanych kilometrów (
) od liczby przejechanych kilometrów (![]() ) wyraża się wzorem
) wyraża się wzorem
![]()
Jaką pojemność ma bak tego samochodu?
Przykład 30 – opisanie funkcji za pomocą wzoru
Most zbudowany jest z przęseł o długości 10 m każde. Przęsło pod wpływem wzrostu temperatury wydłuża się. Przyrost tego wydłużenia jest wprost proporcjonalny do przyrostu temperatury. Wartość przyrostu długości przęsła dla wybranych wartości przyrostu temperatury przedstawia poniższa tabela:
|
przyrost temperatury |
0 |
10 |
30 |
45 |
|
przyrost długości przęsła |
0 |
1 |
3 |
4,5 |
Zapisz zależność długości przęsła (![]() ) od przyrostu temperatury (
) od przyrostu temperatury (![]() ) za pomocą wzoru. Podaj współczynnik proporcjonalności
) za pomocą wzoru. Podaj współczynnik proporcjonalności ![]() do
do ![]() z odpowiednią jednostką.
z odpowiednią jednostką.
Przykład 31 – wybranie układu równań odpowiedniego do opisanej sytuacji.
Rodzice Jacka kupili 36 butelek wody mineralnej o pojemnościach 0,5 litra i 1,5 litra. W sumie zakupili 42 litry wody. Przyjmij, że ![]() oznacza liczbę butelek o pojemności 0,5 litra,
oznacza liczbę butelek o pojemności 0,5 litra, ![]() – liczbę butelek o pojemności 1,5 litra. Który układ równań umożliwi obliczenie, ile zakupiono mniejszych butelek wody mineralnej, a ile większych?
– liczbę butelek o pojemności 1,5 litra. Który układ równań umożliwi obliczenie, ile zakupiono mniejszych butelek wody mineralnej, a ile większych?
A. ![]()
B. ![]()
C. 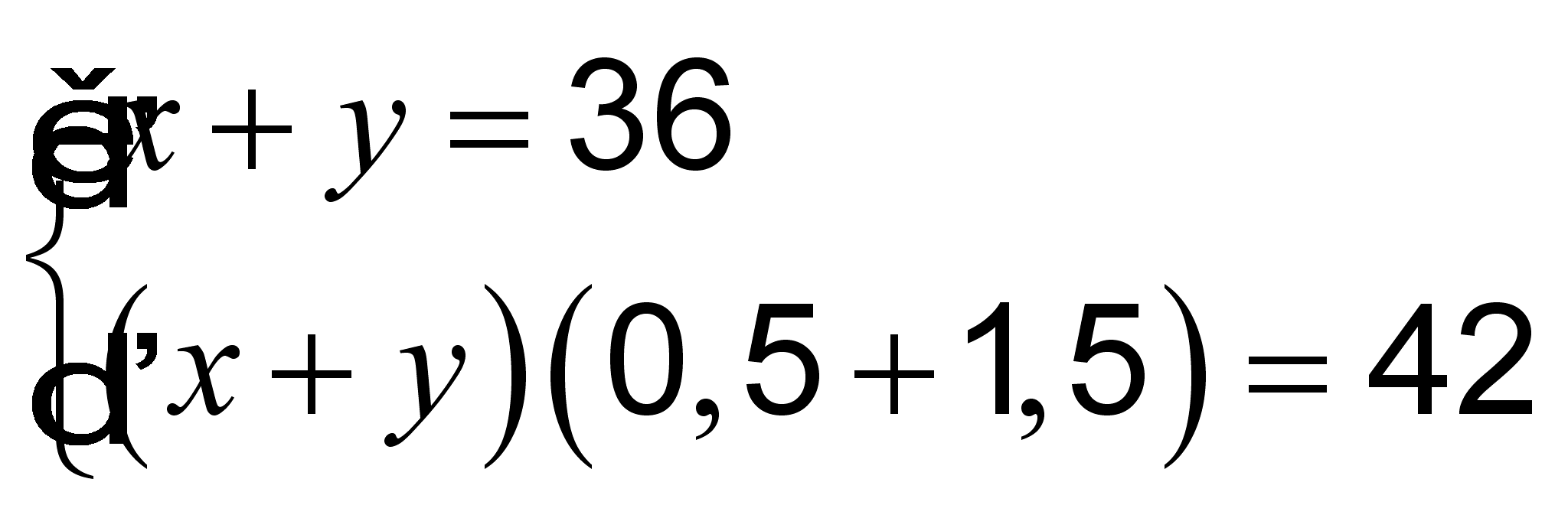
D. ![]()
Przykład 32 – posługiwanie się językiem symboli chemicznych
Na podstawie informacji z poniższego fragmentu tabeli rozpuszczalności soli i wodorotlenków w wodzie wybierz zdanie prawdziwe.
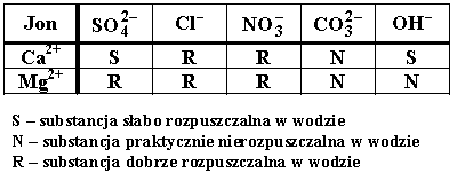
A. Wodorotlenek wapnia słabo rozpuszcza się w wodzie.
B. Wodorotlenek wapnia nie rozpuszcza się w wodzie.
C. W tabeli nie podano informacji o rozpuszczalności wodorotlenku wapnia.
D. Wodorotlenek wapnia dobrze rozpuszcza się w wodzie.
VI umiejętność: stosowanie terminów i pojęć matematyczno – przyrodniczych do opisu zjawisk, właściwości, zachowań, obiektów i organizmów
Przykład 33 – posługiwanie się układem okresowym pierwiastków
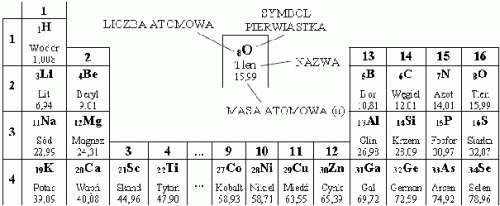
Na podstawie zamieszczonego fragmentu układu ukresowego wybierz zdanie prawdziwe dotyczące sodu ![]() :
:
A. W jądrze atomu sodu jest 11 neutronów.
B. Liczba atomowa sodu jest równa 12.
C. Atom sodu ma konfigurację elektronową: 2, 8, 1.
D. Sód leży w trzecim okresie i drugiej grupie układu okresowego.
Przykład 34 – określanie zmian energii
Na fragmencie poziomicowej mapy terenu górskiego zaznaczone są punkty D, G, K, S i W.
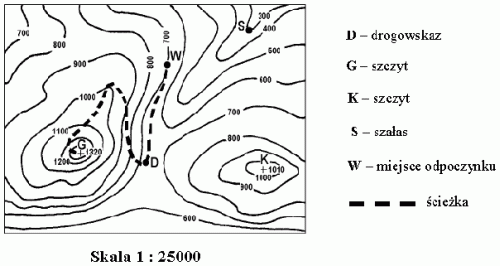
Uczestnicy wycieczki odpoczywający w punkcie W mają pewną energię potencjalną grawitacji. Jak zmieni się ich energia potencjalna grawitacji po wejściu na szczyt G?
A. Zmniejszy się.
B. Zwiększy się.
C. Pozostanie taka sama.
D. Zamieni się na kinetyczną.
Przykład 35 – określanie oddziaływań między organizmami
Określ oddziaływania między populacją mszycy a populacją brzozy.
A. Rywalizują o zasoby środowiska.
B. Obie odnoszą wzajemne korzyści.
C. Nie są zdolne do życia jedna bez drugiej.
D. Jedna z populacji osiąga korzyści, a druga ponosi straty.
Przykład 36 – posługiwanie się skalą mapy
Długość trasy na mapie w skali 1 : 10 000 000 jest równa 7,7 cm. W rzeczywistości trasa ta ma długość
A. 7,7 km
B. 77 km
C. 770 km
D. 7700 km.
Przykład 37 – określanie składu substancji chemicznej
Ile atomów tworzy cząsteczkę wody i ile pierwiastków wchodzi w jej skład?
A. Dwa atomy, trzy pierwiastki.
B. Trzy atomy, dwa pierwiastki.
C. Trzy atomy, jeden pierwiastek.
D. Dwa atomy, dwa pierwiastki.
Przykład 38 – posługiwanie się pojęciami masy i siły
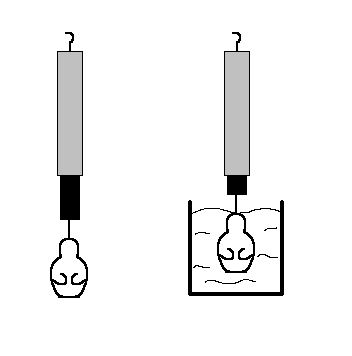
Na siłomierzu zawieszono posążek. Siłomierz wskazywał wtedy wartość 77,3 N. Po zanurzeniu posążka w wodzie wskazanie siłomierza zmniejszyło się do 73 N. Wskaż zdanie prawdziwe.
A. W wodzie masa posążka jest mniejsza niż w powietrzu.
B. W wodzie na posążek działa mniejsza siła grawitacji.
C. W wodzie na posążek oprócz siły grawitacji działa siła wyporu.
D. W wodzie na posążek działa tylko siła wyporu.
Przykład 39 – określanie składników ekosystemu
W ekosystemie wodnym fitoplankton (plankton roślinny) pełni rolę
A. producentów
B. destruentów
C. konsumentów I rzędu
D. konsumentów wyższych rzędów.
Przykład 40 – określanie kierunków geograficznych
W południe słoneczne drzewo stojące pośrodku ogrodu rzuca cień.
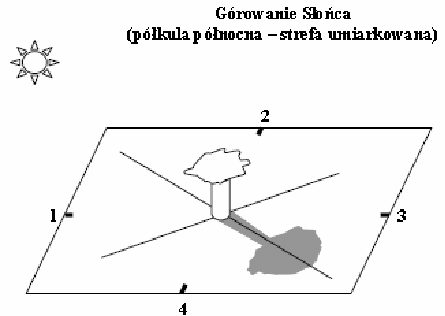
Podpisz w odpowiednich miejscach na rysunku wszystkie główne kierunki geograficzne.
Przykład 41 – określanie stężeń roztworów
Zasolenie Bałtyku wynosi średnio 7,8‰.
Jedna tona średnio zasolonej wody z Morza Bałtyckiego zawiera około
A. 0,078 kg soli
B. 0,78 kg soli
C. 7,8 kg soli
D. 78 kg soli.
Przykład 42 – posługiwanie się własnościami obwodów elektrycznych
Obwód elektryczny składa się z 9 V baterii, amperomierza i trzech identycznych żarówek.
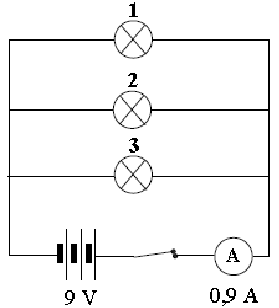
Na podstawie przedstawionego schematu można wnioskować, że
A. żarówka 1 świeci jaśniej niż żarówka 3
B. żarówka 3 świeci jaśniej niż żarówka 1
C. żarówka 2 świeci jaśniej niż żarówki 1 i 3
D. wszystkie żarówki świecą tak samo jasno.
Przykład 43 – opisywanie organizmów
Porosty to organizmy powstające w wyniku symbiozy
A. grzyba i glonu.
B. grzyba i drzewa.
C. grzyba i mchu.
D. dwóch gatunków grzybów.
Przykład 44 – rozpoznawanie formacji roślinnych
Na Ziemi występuje wiele formacji roślinnych, których rozmieszczenie jest w głównej mierze uzależnione od klimatu. Na podstawie opisu rozpoznaj formację roślinną.
Występuje w strefie międzyzwrotnikowej. Rosną tam głównie trawy oraz pojedyncze drzewa, wśród których dominują akacje i baobaby.
A. Tajga
B. Sawanna
C. Step
D. Tundra.
VII umiejętność: stosowanie zintegrowanej wiedzy i umiejętności do rozwiązywania problemów (kojarzenie różnych faktów, wyciąganie wniosków, układanie i realizowanie planu rozwiązania problemu)
Przykład 45 – kojarzenie różnych faktów dotyczących sił działających na ciało
Kropla wody spadająca z chmury poruszała się początkowo ruchem przyspieszonym, a później ruchem jednostajnym. Wybierz rysunki, na których poprawnie przedstawiono siły działające na kroplę wody w początkowej i w końcowej fazie spadania (![]() oznacza siłę oporu powietrza,
oznacza siłę oporu powietrza, ![]() – siłę ciężkości).
– siłę ciężkości).
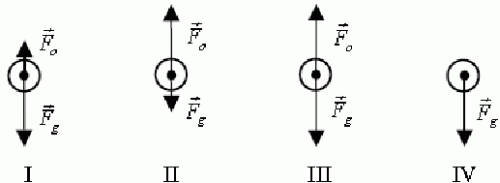
A. Faza początkowa – rysunek II, końcowa – rysunek III
B. Faza początkowa – rysunek I, końcowa – rysunek III
C. Faza początkowa – rysunek II, końcowa – rysunek IV
A. Faza początkowa – rysunek IV, końcowa – rysunek I.
Przykład 46 – powiązanie kształtu bryły z jej objętością
Do początkowo pustych wazonów, takich jak przedstawiono na rysunkach, jednakowym i równomiernym strumieniem wpływała woda.
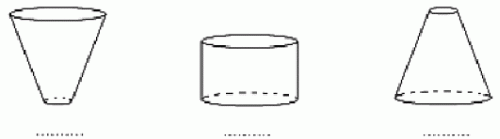
Na wykresach I – IV przedstawiono schematycznie charakter zależności wysokości poziomu wody w wazonie od czasu jego napełniania. Pod każdym wazonem wpisz numer odpowiedniego wykresu.
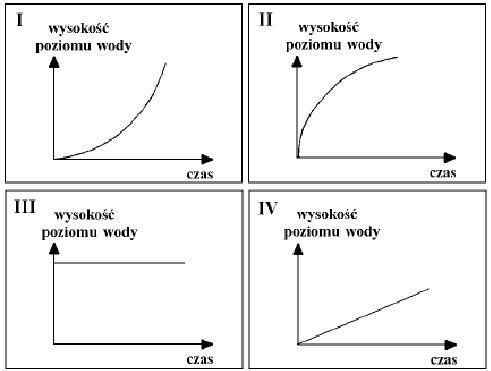
Przykład 47 – obliczanie wartości funkcji opisanej słownie
Na fragmencie poziomicowej mapy terenu górskiego zaznaczone są punkty D, G, K, S i W.
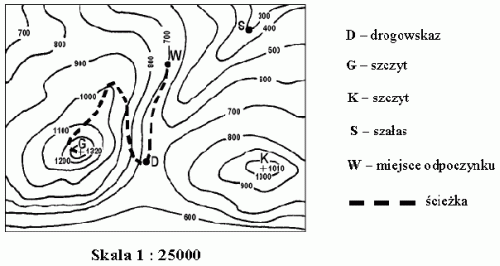
Reguła obliczania czasu przejścia trasy w górach:
Przyjmij 1 godzinę na każde 5 km odczytane (w poziomie) z mapy i dodaj po 1 godzinie na każde 600 m wzniesienia, które trzeba pokonać.
Ścieżka prowadząca od punktu W na szczyt G ma na mapie długość 10 cm. Zgodnie z powyższą regułą wejście tą trasą na szczyt zajmie uczestnikom wycieczki około
A. 1 h
B. 1,5 h
C. 2 h
D. 3 h.
Przykład 48 – określanie zagrożeń dla środowiska
W okresie wiosennym niektórzy rolnicy mimo zakazu wypalają trawę. Podaj dwa negatywne dla środowiska skutki takiego działania.
Przykład 49 – kojarzenie wyników doświadczeń i wyciąganie wniosków
Tomek wykonał doświadczenie, w którym na cynk podziałał kwasem solnym. Probówkę do zbierania wydzielającego się gazu umieścił w wanience z wodą. Rysunek przedstawia schemat tego doświadczenia.
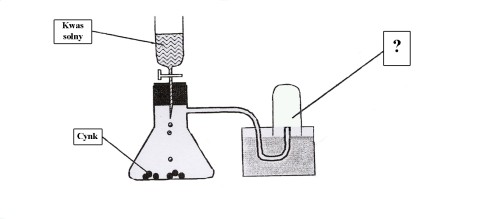
a) Zapisz równanie reakcji zachodzącej w doświadczeniu.
b) Nazwij powstałe produkty reakcji, uzupełniając zdanie:
Produktami reakcji zachodzącej w doświadczeniu są ………………………………….
c) Napisz, w jaki sposób zidentyfikujesz wydzielający się gaz.
Z analizy testów CKE przeprowadzonej przez nauczycieli Firmy "MARKA", wynika, iż pewne zagadnienia w testach egzaminacyjnych w latach 2002-2005 pojawiały się w częściej niż inne. Wielce prawdopodobne, że i w tym roku można spodziewać się tego typu tematów tzw. "pewniaków".
Wiedza i umiejętności potrzebna z zakresu:
- Integrowania wiedzy z różnych działów biologii i dziedzin nauki np. chemii, geografii i fizyki do wyjaśniania zjawisk biologicznych, szczególnie ekologicznych, np. kwaśnych deszczy, efektu cieplarnianego,
- podstawowych form ochrony przyrody w Polsce oraz z zakresu krążenia energii i materii w ekosystemie,
- rozpoznawania na rysunku pospolitych gatunków drzew, krzewów, zbóż i chwastów,
- opisywania i uzupełniania schematów i rysunków, np. dotyczących fotosyntezy, odczytywania informacji z tabeli,
- wyjaśniania związków między budową i funkcją organów oraz układów wewnętrznych człowieka i roślin,
- podstawowych procesów biochemicznych, np. oddychania i fotosyntezy.
Do tej pory rzadziej pojawiały się pytania z genetyki i ewolucji.
Opracowała mgr Izabela Wiśniowska – nauczycielka w LO im. Herberta
Pięć podstawowych umiejętności, których opanowanie jest warunkiem powodzenia na egzaminie gimnazjalnym.
I umiejętność: odczytywanie informacji przedstawionych w różnej formie (mapy, tabeli, wykresu, rysunku, schematu, fotografii, tekstu)
Przykład 1 – odczytanie informacji z mapy
Mapy przedstawiają zasięg i intensywność opadów tego samego dnia o godz. 0.00 i o godz. 6.00.
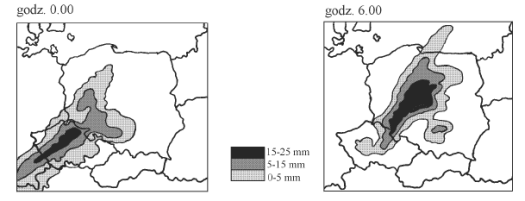
O godzinie 6.00 najobfitsze opady wystąpiły w
- A. Łodzi i Krakowie
- B. Białymstoku i Wrocławiu
- C. Łodzi i Wrocławiu
- D. Gdańsku i Szczecinie.
Odpowiedź: C (w Łodzi i Wrocławiu)
Przykład 2 – odczytanie informacji z diagramu kołowego
Diagram przedstawia procentowy udział powierzchni poszczególnych kontynentów w całkowitej powierzchni lądów.
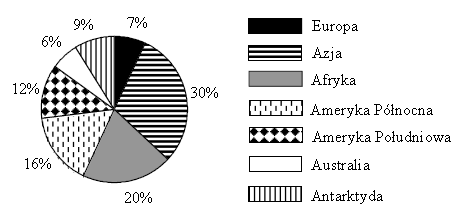
Które zdanie jest prawdziwe?
- A. Ameryka Północna i Azja zajmują łącznie więcej niż połowę lądów Ziemi.
- B. Europa ma najmniejszą powierzchnię spośród wszystkich kontynentów.
- C. Afryka i Azja mają łącznie większą powierzchnię niż pozostałe lądy Ziemi.
- D. Powierzchnia Azji stanowi mniej niż jedną trzecią powierzchni lądów Ziemi.
Odpowiedź: D
Przykład 3 – odczytanie informacji z wykresu
Wykres ilustruje zmiany temperatury gleby w pewnej miejscowości na głębokości 10 cm i 30 cm w ciągu doby w okresie lata.
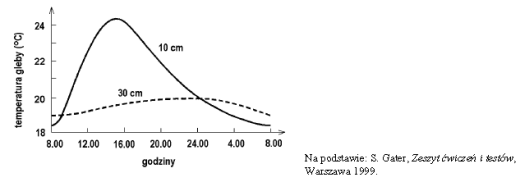
Jaką temperaturę ma gleba w południe na głębokości 10 cm?
- A. Niższą niż 21°C.
- B. Między 22°C a 23°C.
- C. Między 23°C a 24°C.
- D. Wyższą niż 24°C.
Odpowiedź: B
Przykład 4 – odczytanie informacji z tabeli
Filip zamieścił na swojej stronie internetowej następujące informacje dotyczące planet Układu Słonecznego:
| Lp. | Nazwa planety | Masa planety w stosunku do masy Ziemi | Liczba księżyców |
|---|---|---|---|
| 1 | Merkury | 0,06 | 0 |
| 2 | Wenus | 0,82 | 0 |
| 3 | Ziemia | 1 | 1 |
| 4 | Mars | 0,11 | 2 |
| 5 | Jowisz | 317,9 | 16 |
| 6 | Saturn | 95,18 | 20 |
| 7 | Uran | 14,5 | 17 |
| 8 | Neptun | 17,24 | 8 |
| 9 | Pluton | 0,002 | 1 |
Tablice geograficzne, Wyd. Adamantan, Warszawa 1998
Która z planet o masie mniejszej niż masa Ziemi ma najwięcej księżyców?
- A. Mars
- B. Saturn
- C. Neptun
- D. Pluton.
Odpowiedź: A
Przykład 5 – odczytanie informacji z diagramu słupkowego
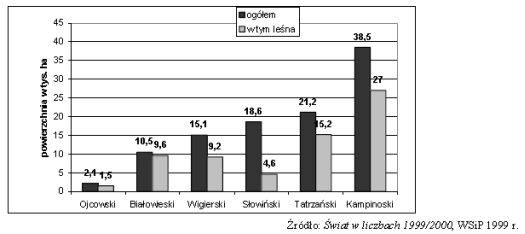
Całkowita powierzchnia Parku Tatrzańskiego jest większa od całkowitej powierzchni Parku Białowieskiego o
- A. 16,3 tys. ha
- B. 11,7 tys. ha
- C. 10,7 tys. ha
- D. 5,6 tys. ha.
Odpowiedź C
{mospagebreak title=umiejętność II&heading=umiejętność I}
pięć podstawowych umiejętności, których opanowanie jest warunkiem powodzenia na egzaminie gimnazjalnym
II umiejętność: operowanie informacjami (ich selekcja, analizowanie, przetwarzanie, interpretowanie, wykorzystywanie w praktyce)
Przykład 6 – przetworzenie informacji zawartych w tabeli
Tabela przedstawia ceny kart wstępu na pływalnię. Czas pływania uwzględnia liczbę wejść oraz czas jednego pobytu na basenie.
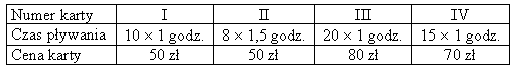
Godzina pływania jest najtańsza przy zakupie karty:
- A. I
- B. II
- C. III
- D. IV
Odpowiedź: C
Przykład 7 – przetworzenie informacji zawartych na rysunku
Na podstawie poniższego rysunku wyznacz objętość kamienia wrzuconego do wody:
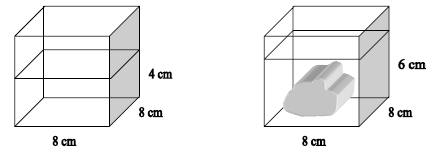
- A. 256 cm3
- B. 128 cm3
- C. 384 cm3
- D. 488 cm3
Odpowiedź: B
Przykład 8 – przetworzenie informacji zawartych na wykresie
Wykres przedstawia zależność rozpuszczalności dwutlenku węgla w wodzie od temperatury.
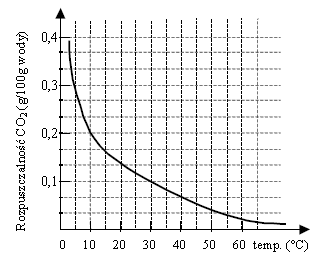
100 g wody o temperaturze 5ºC nasycono dwutlenkiem węgla. Ile gramów CO2 wydzieli się w postaci gazu, gdy ten roztwór ogrzejemy do temperatury 30ºC?
- A. 0,1
- B. 0,2
- C. 0,3
- D. 0,4
Odpowiedź: B
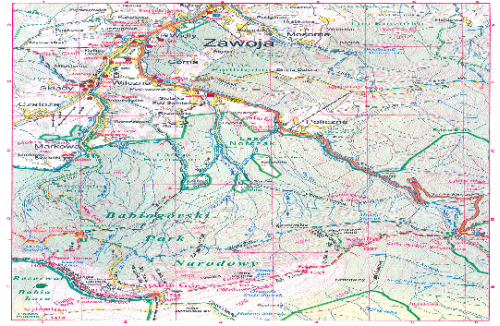
Przykład 9 – przetworzenie informacji zawartych na mapie
Na mapie przedstawiono trasę rejsu statku płynącego do Kołobrzegu.
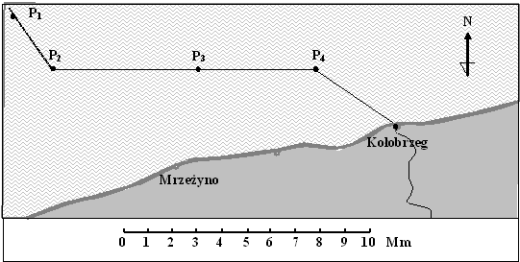
Pewnego dnia zasięg światła kołobrzeskiej latarni morskiej wynosił 10 Mm. Najbardziej oddalonym od Kołobrzegu punktem, spośród zaznaczonych na trasie statku, z którego można było tego dnia dostrzec światło latarni, był punkt:
- A. P1
- B. P2
- C. P3
- D. P4
Odpowiedź: C
Przykład 10 – przetworzenie informacji zawartych na diagramach
W Londynie ogromnym problemem jest smog, składający się między innymi z tlenków siarki i tlenków azotu. Pewnego dnia w atmosferze znalazła się taka sama masa tlenków siarki co tlenków azotu. Diagramy przedstawiają źródła zanieczyszczeń powietrza tymi tlenkami.


Największa łączna masa wyemitowanych tlenków azotu i tlenków siarki pochodziła z
- A. transportu
- B. gospodarstw domowych
- C. energetyki
- D. przemysłu (w tym rafinerii).
Odpowiedź: C
{mospagebreak title=umiejętność III}
pięć podstawowych umiejętności, których opanowanie jest warunkiem powodzenia na egzaminie gimnazjalnym
III umiejętność: wykonywanie obliczeń w sytuacjach praktycznych
Przykład 11 – wykonanie obliczeń na liczbach dziesiętnych
Montaż instalacji gazowej w samochodzie kosztuje 2208 zł. Samochód spala średnio 7 litrów benzyny lub 8 litrów gazu na każde 100 km drogi. Oblicz, po ilu miesiącach zwrócą się koszty instalacji, jeśli w ciągu miesiąca samochód przejeżdża średnio 2000 km. Zapisz obliczenia.
| Cena benzyny | Cena gazu |
|---|---|
| 3,8 zł/l | 1,6 zł/l |
Odpowiedź: Po 8 miesiącach.
Przykład 12 – operowanie procentami
| Hurtownia „O. WOC i SYN” ceny (w zł) za 1 kg |
||
|---|---|---|
| Rodzaj owoców | Gatunek I | Gatunek II |
| Jabłka | 2,40 | 1,80 |
| Gruszki | 4,00 | 3,60 |
| Cytryny | 3,20 | 2,40 |
| Pomarańcze | 2,60 | 2,20 |
| Mandarynki | 4,80 | 4,20 |
Cena 1 kg jabłek II gatunku jest mniejsza od ceny 1 kg tych owoców I gatunku o
- A. 60%
- B. 25%
- C. 33%
- D. 30%
Odpowiedź: B
Przykład 13 – operowanie procentami
Uzupełnij rachunek wystawiony przez firmę budowlaną, wpisując w wykropkowanych miejscach obliczone wartości:

Odpowiedź: 
Przykład 14 – posługiwanie się jednostkami miar i przybliżeniami
Wieża Eiffla znajduje się na obszarze w kształcie kwadratu o boku długości 125 m. Ile hektarów powierzchni ma ten obszar? Wynik podaj z dokładnością do 0,1 ha.
Odpowiedź: 1,6 ha
Przykład 15 – posługiwanie się jednostkami miar
W tablicach geograficznych podano następujące określenia roku:

Tablice geograficzne. Wydawnictwo Adamantan, Warszawa 1998
Wybierz odpowiedź na pytanie: o ile rok gwiazdowy jest dłuższy od zwrotnikowego?
- A. o 1 h 39 min 36 s
- B. o 1 h 57 min 56 s
- C. o 57 min 36 s
- D. o 20 min 24 s.
Odpowiedź: D
{mospagebreak title=umiejętność IV}
pięć podstawowych umiejętności, których opanowanie jest warunkiem powodzenia na egzaminie gimnazjalnym
IV umiejętność: posługiwanie się własnościami figur
Przykład 16 – zauważanie symetrii figur geometrycznych
(zadanie z próbnego egzaminu gimnazjalnego przeprowadzonego przez OKE Warszawa w styczniu 2006 r.)
Przedstawiona na rysunku flaga Wielkiej Brytanii

- A. ma cztery osie symetrii i środek symetrii.
- B. ma cztery osie symetrii i nie ma środka symetrii.
- C. ma dwie osie symetrii i środek symetrii.
- D. ma dwie osie symetrii i nie ma środka symetrii.
Odpowiedź: C
Przykład 17 – obliczanie obwodów figur płaskich
Odczytaj dane potrzebne do obliczeń z rysunku i wskaż liczbę, która jest równa obwodowi powstałej figury.
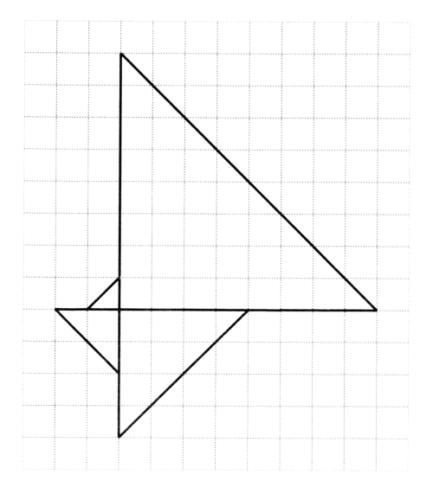
- A. 10 + √2
- B. 11√2
- C. 12
- D. 15√2 + 14
Odpowiedź: D
Przykład 18 – obliczanie pól powierzchni figur płaskich
Na miejscu dawnego skrzyżowania postanowiono wybudować rondo, którego wymiary (w metrach) podane są na rysunku.

Oblicz, na jakiej powierzchni trzeba wylać asfalt (obszar zacieniowany na rysunku). W swoich obliczeniach za π podstaw 22/7.
Odpowiedź: 462 m2
Przykład 19 – obliczanie pól powierzchni i objętości brył
(zadanie z próbnego egzaminu gimnazjalnego przeprowadzonego przez OKE Wrocław w marcu 2004 r.)
Serek ma kształt graniastosłupa, którego podstawą jest trójkąt o długościach boków: 8 cm, 8 cm i 3 cm. Wojtek i Ewa postanowili podzielić serek na dwie części o równych objętościach. Wojtek lubi skórkę pokrywającą całą powierzchnię serka, więc zaproponował cięcie jak na rysunku. Czy rzeczywiście obie części mają tę samą objętość? Która część ma większą powierzchnię ze skórką? 
Odpowiedź: Obie części mają taka samą objętość. Większą powierzchnię ze skórką ma część I.
Przykład 20 – obliczanie pól powierzchni i objętości brył
Do naczynia w kształcie prostopadłościanu o wymiarach 2 dm × 1,5 dm × 12 cm wypełnionego całkowicie wodą włożono sześcienną metalową kostkę, której pole powierzchni całkowitej jest równe 600 cm2. Oblicz, ile litrów wody pozostało w tym naczyniu.
Odpowiedź: 2,6 litra.
{mospagebreak title=umiejętność V}
pięć podstawowych umiejętności, których opanowanie jest warunkiem powodzenia na egzaminie gimnazjalnym
V umiejętność: posługiwanie się językiem symboli i wyrażeń algebraicznych oraz funkcjami (zapisywanie wielkości za pomocą wyrażeń algebraicznych, przekształcanie wyrażeń algebraicznych, zapisywanie związków między wielkościami za pomocą równań)
Przykład 21 – przekształcanie wyrażeń algebraicznych
W połączeniu równoległym oporników opór zastępczy (całkowity) można wyrazić wzorem ![]() . Który wzór pozwala obliczyć opór R1 pierwszego opornika?
. Który wzór pozwala obliczyć opór R1 pierwszego opornika?
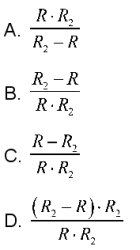
Odpowiedź: A
Przykład 22 – układanie równań lub układów równań
Trzy lata temu posadzono przed domem krzew. Co roku podwajał on swoją wysokość i teraz ma 144 cm. Jeśli przez x oznaczymy wysokość krzewu w dniu posadzenia, to informacjom z zadania odpowiada równanie:
- A. x = 114
- B. 4x = 114
- C. 6x = 114
- D. 8x = 114
Odpowiedź: D
Przykład 23 – ułożenie i rozwiązanie równania lub układu równań („zadania tekstowe”)
Na rzece zbudowano most, który zachodzi na jej brzegi: 150 m mostu zachodzi na jeden brzeg, a 1/3 długości mostu na drugi. Oblicz szerokość rzeki, jeżeli stanowi ona 1/6 długości mostu.
Odpowiedź: 50 m
Przykład 24 – analizowanie podanych funkcji
Obserwując zużycie benzyny w swoim samochodzie pan Nowak stwierdził, że jeśli wystartuje z pełnym bakiem i będzie jechał po autostradzie ze stałą prędkością, to zależność liczby litrów benzyny w baku (y) od liczby przejechanych kilometrów (x) wyraża się wzorem
y = -0,05x + 45
Jaką pojemność ma bak tego samochodu?
Odpowiedź: Odpowiedź: 45 litrów.
Przykład 25 – opisanie funkcji za pomocą wzoru
Most zbudowany jest z przęseł o długości 10 m każde. Przęsło pod wpływem wzrostu temperatury wydłuża się. Przyrost tego wydłużenia jest wprost proporcjonalny do przyrostu temperatury. Wartość przyrostu długości przęsła dla wybranych wartości przyrostu temperatury przedstawia poniższa tabela:
| przyrost temperatury Δt (°C) | 0 | 10 | 30 | 45 |
|---|---|---|---|---|
| przyrost długości przęsła Δl (mm) | 0 | 1 | 3 | 4,5 |
Zapisz zależność długości przęsła (Δl) od przyrostu temperatury (Δt) za pomocą wzoru. Podaj współczynnik proporcjonalności Δl do Δt z odpowiednią jednostką.
Odpowiedź: Δl = 0,1·Δt, współczynnik = 0,1 mm·°C-1 = 10-4 m·°C-1