Z analizy testów CKE przeprowadzonej przez nauczycieli Firmy "MARKA", wynika, iż pewne zagadnienia w testach egzaminacyjnych w latach 2002-2008 pojawiały się w częściej niż inne. Wielce prawdopodobne, że i w tym roku można spodziewać się tego typu tematów tzw. "pewniaków".

1. umiejętność sprawnego wykonywania działań arytmetycznych na liczbach rzeczywistych (dodawania, odejmowania, mnożenia i dzielenia ułamków zwykłych i dziesiętnych)

   Przykład:
   Masa kości szkieletu ciała ludzkiego wynosi 9800 g. Jaka jest (w przybliżeniu) całkowita masa tego człowieka, jeżeli wiadomo, że masa szkieletu stanowi 0,17 masy całego ciała?

   Odpowiedź: 57,6 kg.

2. umiejętność operowania procentami w rozmaitych sytuacjach praktycznych

   Przykład:
   W Kampinoskim Parku Narodowym lasy zajmują powierzchnię 27 tys. ha, zaś w Tatrzańskim Parku Narodowym – powierzchnię 15,2 tys. ha. O ile procent więcej lasów jest w Puszczy Kampinoskiej niż w Tatrach?

   Odpowiedź: O około 78%.

3. umiejętność odczytywania informacji przedstawionych w rozmaitych formach (tabeli, diagramu, rysunku) i przetwarzania tych informacji

   Przykład:
   Oto wyniki krótkiego sprawdzianu przeprowadzonego w trzech oddziałach III klasy gimnazjum:

   

   

   

   Z wykresów tych wynika, że sprawdzian był:
   A. najtrudniejszy dla uczniów z III a
   B. najtrudniejszy dla uczniów z III b
   C. najtrudniejszy dla uczniów z III c
   D. jednakowo trudny dla uczniów ze wszystkich trzech klas

   Odpowiedź: A.

4. umiejętność przekształcania wyrażeń algebraicznych

   Przykład:
   Ze wzoru opisującego pole powierzchni prostopadłościanu: P=2(ab+bc+ac) wyznacz a.

   Odpowiedź: .

5. umiejętność zapisania treści zadania za pomocą układu równań oraz rozwiązania tego układu równań (czyli tzw. "zadania tekstowe")

   Przykład:
   W III klasie pewnego gimnazjum przeprowadzony został test. Test zawierał 100 pytań; za prawidłową odpowiedź uczeń otrzymywał 2 punkty, za złą (-1) punkt, a za brak odpowiedzi 0 punktów. Po sprawdzeniu testu okazało się, że uczeń nie udzielił 20 odpowiedzi i łącznie uzyskał 100 punktów. Ile było odpowiedzi dobrych, a ile błędnych?

   Odpowiedź: 60 dobrych i 20 błędnych.

6. umiejętność posługiwania się własnościami figur geometrycznych i rozpoznawania symetrii

   Przykład:
   Na zabawę przygotowano ciastka o różnych kształtach. Które ciastka mają dokładnie 5 osi symetrii?

   

   A. 2 i 3
   B. 3 i 4
   C. 4 i 5
   D. 3 i 5

   Odpowiedź: B.

7. umiejętność stosowania twierdzenia Pitagorasa

   Przykład:
   Trawnik ma kształt czworokąta, jak na rysunku: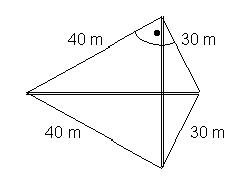

   

   Jaką długość mają przecinające trawnik ścieżki (zaznaczone na rysunku podwójnymi liniami)? Odpowiedź: 48 cm i 50 cm.

8. umiejętność obliczania obwodów i pól powierzchni figur płaskich

   Przykład:
   Pień starego dębu ma na pewnej wysokości obwód 6,3 m. Jaka jest średnica pnia? (Wynik podaj z dokładnością do 10 cm).

   Odpowiedź: 200 cm.

9. umiejętność obliczania objętości i pól powierzchni brył

   Przykład:
   Do prostopadłościennego akwarium o wymiarach 5 dm × 30 cm × 25 cm, całkowicie wypełnionego wodą, włożono sześcienną ołowianą kostkę, której pole powierzchni całkowitej wynosi 600 cm². Ile litrów wody pozostało w akwarium po wrzuceniu kostki?

   Odpowiedź: 36,5 litra.

10. umiejętność stosowania tzw. "technik twórczego rozwiązywania problemów" (czyli samodzielne sformułowanie hipotezy – lub wybranie jednej z przedstawionych hipotez – i próba jej uzasadnienia)

    Przykład:
    Na gałązce świerku każdego roku wyrastają z nowego pąka 3 nowe pędy zakończone pąkiem. Ile pąków będzie miała po dziewięciu latach świerkowa gałązka, która wyrosła z jednego pąka?

    A. 3·9
    B. 3+9
    C. 9³
    D. 3⁹

    Odpowiedź: D.

Opracował mgr Krzysztof Zawadzki – nauczyciel Firmy "MARKA"

 

Sprawdź kursy przygotowawcze w Warszawie – www.marka.edu.pl