25.02.2009
Siedem podstawowych umiejętności egzaminacyjnych
Analiza testów CKE z lat 2002-2012 przeprowadzonej przez nauczycieli Firmy Edukacyjnej Marka wynika nie tylko powtarzalność pewnych zagadnień , ale także kluczowe znaczenie pewnych umiejętności, bez których gimnazjalista nie ma co marzyć o sukcesie na egzaminach z poszczególnych przedmiotów. Jeżeli nie wiecie od czego zacząć swoją powtórkę, to idźcie drogą wskazaną przez autora tego opracowania, p.Krzysztofa Zawadzkiego – nauczyciela Firmy Edukacyjnej Marka, który od ponad 20 lat przygotowuje do egzaminów. Powodzenia!
I umiejętność: odczytywanie informacji przedstawionych w różnej formie (mapy, tabeli, wykresu, rysunku, schematu, fotografii, tekstu)
Przykład 1 – odczytanie informacji z mapy
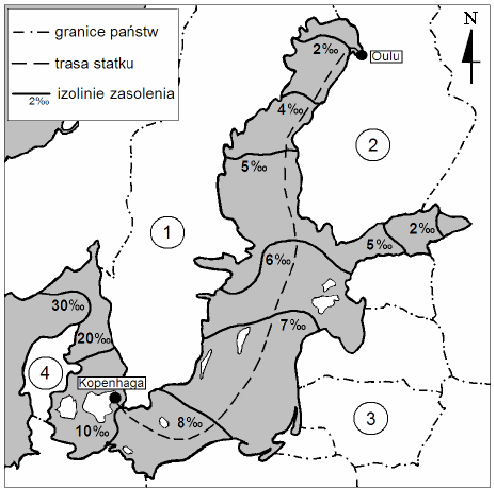
Zasolenie morza określa się jako ilość gramów soli rozpuszczonych w jednym kilogramie wody morskiej i podaje w promilach (‰). Przeciętnie w jednym kilogramie wody morskiej znajduje się 34,5 g różnych rozpuszczonych w niej soli (czyli przeciętne zasolenie wody morskiej jest równe 34,5‰).
Zasolenie Bałtyku (średnio 7,8‰) jest znacznie mniejsze od zasolenia oceanów, co tłumaczy się wielkością zlewiska (duży dopływ wód rzecznych), warunkami klimatycznymi (małe parowanie) oraz utrudnioną wymianą wód z oceanem.
|
Zasolenie Morza Bałtyckiego |
|
|
Na podstawie: J. Kondracki, Geografia fizyczna Polski, Warszawa 1988
Zasolenie zmieniające się od 2‰ do ponad 20‰ mają wody wzdłuż wybrzeża państwa, które na rysunku oznaczono liczbą
A. 1
B. 2
C. 3
D. 4
Przykład 2 – odczytanie informacji z diagramu kołowego
Poważnym problemem są zanieczyszczenia Bałtyku substancjami biogennymi. Diagramy przedstawiają procentowy udział państw nadbałtyckich w zanieczyszczeniu Morza Bałtyckiego związkami azotu (diagram a) i związkami fosforu (diagram b) w 1995 roku.
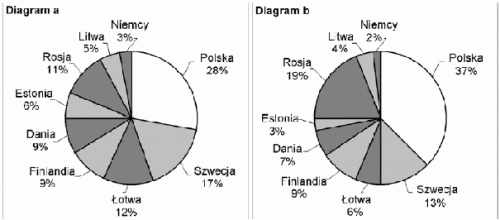
Na podstawie: www.naszbaltyk.pl
Procentowy udział Polski w zanieczyszczeniu Bałtyku związkami azotu w 1995 r. był taki, jak łącznie krajów
A. Szwecji i Rosji
B. Rosji i Łotwy
C. Danii i Finlandii
D. Rosji i Finlandii.
Przykład 3 – odczytanie informacji z wykresu
Na wykresach przedstawiono zależność rozpuszczalności wybranych substancji w wodzie od temperatury.
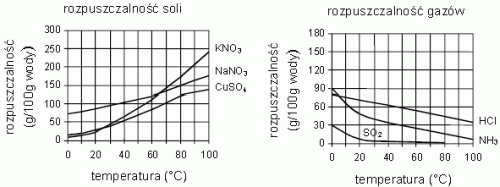
Na podstawie: W. Mizerski, Tablice chemiczne, Warszawa 2003
Korzystając z wykresów, uzupełnij zdania:
Ze wzrostem temperatury rozpuszczalność soli ………………………….. (rośnie / maleje), a gazów ………………………….. (rośnie / maleje). W 100 g wody o temperaturze 500C można rozpuścić co najwyżej ……………………… g NH3.
Przykład 4 – odczytanie informacji z tablicy
Filip zamieścił na swojej stronie internetowej następujące informacje dotyczące planet Układu Słonecznego:
|
Lp. |
Nazwa planety |
Masa planety w stosunku do masy Ziemi |
Liczba księżyców |
|
1. |
Merkury |
0,06 |
0 |
|
2. |
Wenus |
0,82 |
0 |
|
3. |
Ziemia |
1 |
1 |
|
4. |
Mars |
0,11 |
2 |
|
5. |
Jowisz |
317,9 |
16 |
|
6. |
Saturn |
95,18 |
20 |
|
7. |
Uran |
14,5 |
17 |
|
8. |
Neptun |
17,24 |
8 |
|
9. |
Pluton |
0,002 |
1 |
Tablice geograficzne, Wyd. Adamantan, Warszawa 1998
Która z planet o masie mniejszej niż masa Ziemi ma najwięcej księżyców?
A. Mars
B. Saturn
C. Neptun
D. Pluton.
Przykład 5 – odczytanie informacji z diagramu słupkowego
Uczniowie klas trzecich pewnego gimnazjum urządzili w swoich salach wystawy przedstawiające najciekawsze miejsca w różnych krajach. Po obejrzeniu wszystkich ekspozycji przeprowadzona została ankieta, w której uczniowie odpowiadali na pytanie, który kraj chcieliby odwiedzić. Każdy z ankietowanych mógł wybrać tylko jeden kraj.
Oto jakich wyborów dokonali uczniowie.
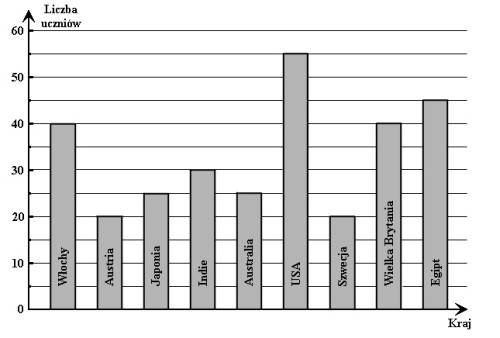
Ilu uczniów uczestniczyło w ankiecie?
A. 310
B. 300
C. 290
D. 250.
II umiejętność: operowanie informacjami (ich selekcja, analizowanie, przetwarzanie, interpretowanie, wykorzystywanie w praktyce)
Przykład 6 – przetworzenie informacji zawartych w tabeli
Tabela przedstawia ceny kart wstępu na pływalnię. Czas pływania uwzględnia liczbę wejść oraz czas jednego pobytu na basenie.
|
Numer karty |
I |
II |
III |
IV |
|
Czas pływania |
10 x 1 godz. |
8 x 1,5 godz. |
20 x 1 godz. |
15 x 1 godz. |
|
Cena karty |
50 zł |
50 zł |
80 zł |
70 zł |
Godzina pływania jest najtańsza przy zakupie karty:
A. I
B. II
C. III
D. IV.
Przykład 7 – przetworzenie informacji zawartych na rysunku
Na podstawie poniższego rysunku wyznacz objętość kamienia wrzuconego do wody:
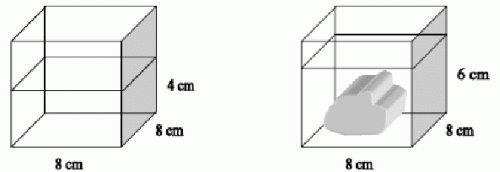
A. 256 cm3
B. 128 cm3
C. 384 cm3
D. 488 cm3.
Przykład 8 – przetworzenie informacji zawartych na wykresie
Wykres przedstawia zależność rozpuszczalności dwutlenku węgla w wodzie od temperatury.
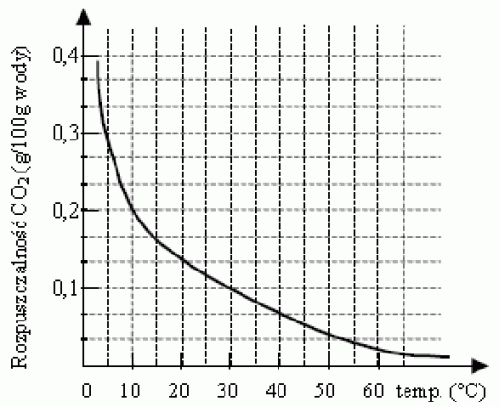
100 g wody o temperaturze 50C nasycono dwutlenkiem węgla. Ile gramów CO2 wydzieli się w postaci gazu, gdy ten roztwór ogrzejemy do temperatury 300C?
A. 0,1
B. 0,2
C. 0,3
D. 0,4.
Przykład 9 – przetworzenie informacji zawartych na mapie
Na mapie zaznaczono 10 krajów, które przystąpiły do Unii Europejskiej 1 maja 2004 roku. Ich powierzchnię podano w tys. km2.
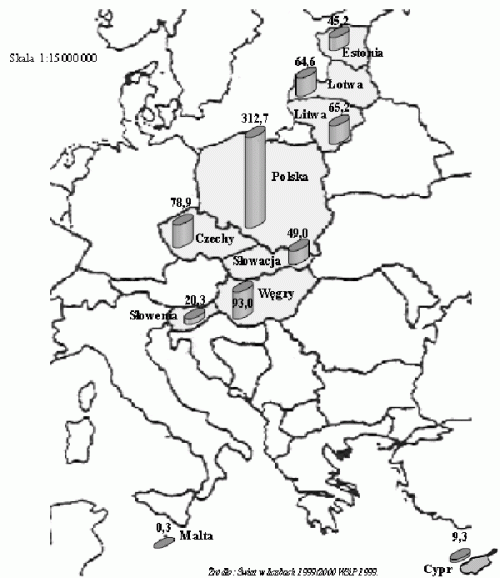
Powierzchnia najmniejszego z tych państw jest mniejsza od powierzchni największego państwa około
A. 15 razy
B. 1042 razy
C. 30 razy
D. 6 razy.
Przykład 10 – przetworzenie informacji zawartych na diagramach
W Londynie ogromnym problemem jest smog, składający się między innymi z tlenków siarki i tlenków azotu. Pewnego dnia w atmosferze znalazła się taka sama masa tlenków siarki co tlenków azotu. Diagramy przedstawiają źródła zanieczyszczeń powietrza tymi tlenkami.
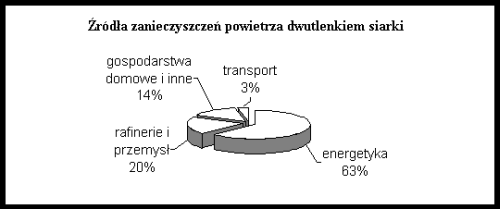
Największa łączna masa wyemitowanych tlenków azotu i tlenków siarki pochodziła z
A. transportu
B. gospodarstw domowych
C. energetyki
D. przemysłu (w tym rafinerii).
Przykład 11 – przetworzenie informacji zawartych w tekście
Biedronki siedmiokropki polują na mszyce w ogrodach i na polach. Mszyce zabezpieczają się przed nimi, wydzielając obronną ciecz, same natomiast żywią się sokiem wyssanym z roślin. Aby ochronić się przed mszycami, rośliny wytwarzają kolce i parzące włoski, które nie zawsze jednak są dostatecznym zabezpieczeniem.
W jaki sposób konsumenci I rzędu, o których mowa w powyższej informacji, bronią się przed naturalnymi wrogami?
Odpowiedź: …………………………………………………………………………………………………….
III umiejętność: wykonywanie obliczeń w sytuacjach praktycznych
Przykład 12 – wykonanie obliczeń na liczbach dziesiętnych
(zadanie z egzaminu gimnazjalnego przeprowadzonego przez CKE w kwietniu 2005 r.)
Montaż instalacji gazowej w samochodzie kosztuje 2208 zł. Samochód spala średnio 7 litrów benzyny lub 8 litrów gazu na każde 100 km drogi. Oblicz, po ilu miesiącach zwrócą się koszty instalacji, jeśli w ciągu miesiąca samochód przejeżdża średnio 2000 km. Zapisz obliczenia.
| cena benzyny | cena gazu |
|---|---|
| 3,80 zł/l | 1,60 zł/l |
Przykład 13 – operowanie procentami
Uzupełnij rachunek wystawiony przez firmę budowlaną, wpisując w wykropkowanych miejscach obliczone wartości:
|
|
Liczba sztuk |
Cena netto |
VAT (22% ceny netto) |
Razem |
|
Okno |
1 |
1200 zł |
………………….. |
……………. |
|
Drzwi |
1 |
………………. |
………………. |
3538 zł |
Przykład 14 – posługiwanie się jednostkami miar i przybliżeniami
Rysunki przedstawiają wskazania wodomierza w dniach 1 września i 1 października.
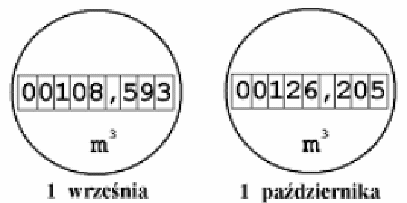
Oblicz, zaokrąglając do całości, ile metrów sześciennych wody zużyto od 1 września do 1 października.
A. 16 m3
B. 17 m3
C. 18 m3
D. 22 m3.
Przykład 15 – posługiwanie się jednostkami miary
Plan kortu tenisowego wykonany w skali 1 : 2000 ma powierzchnię 1 cm2. Jaka jest rzeczywista powierzchnia tego kortu?
A. 2000 m2
B. 20 m2
C. 400 m2
D. 4000 m2.
Przykład 16 – stosowanie własności działań w praktyce
Uczniowie wraz z opiekunami pojechali na wycieczkę do Brukseli. Zwiedzanie Brukseli (520N, 40E) zakończyło się o godzinie 18.00 czasu słonecznego. Która godzina czasu słonecznego była wówczas w Warszawie (520N, 210E)? Zapisz obliczenia.
Przykład 17 – posługiwanie się proporcjami do obliczenia ilości składników mieszaniny
Aby przygotować suchą zaprawę do tynkowania ścian, należy zmieszać piasek, wapno i cement odpowiednio w stosunku 15 : 4 : 1. W którym wierszu tabeli podane są właściwe ilości składników potrzebnych do otrzymania 140 kg takiej zaprawy?
|
|
Piasek (kg) |
Wapno (kg) |
Cement (kg) |
|
I |
101 |
32 |
8 |
|
II |
109 |
24 |
7 |
|
III |
105 |
28 |
7 |
|
IV |
105 |
56 |
14 |
A. I
B. II
C. III
D. IV.
Przykład 18 – obliczanie średniej arytmetycznej liczb
Przez 3 godziny Jacek z Magdą obserwowali ruch samochodowy na moście. Liczyli przejeżdżające pojazdy. Wyniki zapisali w tabeli.
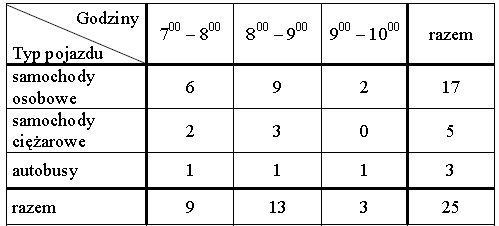
Ile samochodów osobowych przejeżdżało średnio przez most w ciągu jednej godziny obserwacji?
A. 
B. 6
C. 
D. 7.
Przykład 19 – obliczanie kosztu zużytej energii elektrycznej
W ciągu 30 dni w czajniku o mocy 1600 W podgrzewano wodę średnio przez 15 minut dziennie. Oblicz koszt energii elektrycznej zużytej przez czajnik w ciągu tych 30 dni. Przyjmij, że cena 1 kWh energii wynosi 32 gr. Zapisz obliczenia.
IV umiejętność: posługiwanie się własnościami figur
Przykład 20 – zauważanie symetrii figur geometrycznych
Przedstawiona na rysunku flaga Wielkiej Brytanii
A. ma cztery osie symetrii i środek symetrii.
B. ma cztery osie symetrii i nie ma środka symetrii.
C. ma dwie osie symetrii i środek symetrii.
D. ma dwie osie symetrii i nie ma środka symetrii.
Przykład 21 – obliczanie obwodów figur płaskich
Rowerzysta policzył, że podczas jazdy z domu do szkoły koło jego roweru o średnicy 64 cm wykonało 250 obrotów. Przybliżona odległość z domu do szkoły wynosi (
3)
A. 480 m
B. 960 m
C. 7680 m
D. 30720 m.
Przykład 22 – obliczanie pól powierzchni figur płaskich
Przekrój poprzeczny ziemnego wału przeciwpowodziowego ma mieć kształt równoramiennego trapezu o podstawach długości 6 m i 16 m oraz wysokości 12 m. Trzeba jednak usypać wyższy wał, bo przez dwa lata ziemia osiądzie i wysokość wału zmniejszy się o 20% (szerokość wału u podnóża i na szczycie nie zmienia się).
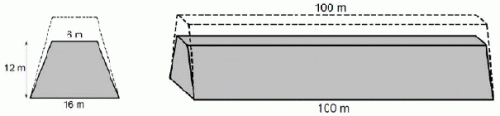
Po zakończeniu osiadania ziemi, w celu zmniejszenia przesiąkania, na zboczu wału od strony wody zostanie ułożona warstwa gliny. Oblicz pole powierzchni, którą trzeba będzie wyłożyć gliną na 100-metrowym odcinku tego wału (wał ma kształt graniastosłupa prostego). Zapisz obliczenia. Wynik podaj z jednostką.
Przykład 23 – obliczanie pól powierzchni brył
Na dziedzińcu przed Luwrem zbudowano szklaną piramidę. Piramida ta ma kształt ostrosłupa prawidłowego czworokątnego o wysokości około 20 metrów i krawędzi podstawy 30 metrów. Wykonaj rysunek pomocniczy wraz z oznaczeniami i oblicz powierzchnię ścian bocznych szklanej piramidy. Zapisz obliczenia.
Przykład 24 – obliczanie objętości brył
Objętość beczki oblicza się wg wzoru: 
, gdzie 
średnica w miejscu najszerszym, 
średnica dna, 
wysokość beczki.
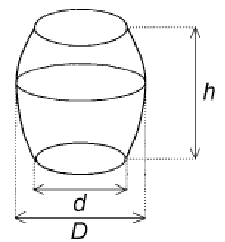
Wojtek obmierzył beczkę w ogrodzie. Ma ona wysokość 12 dm i średnicę dna równą 7 dm. Z powodu trudności ze zmierzeniem średnicy w najszerszym miejscu Wojtek zmierzył obwód w najszerszym miejscu. Jest on równy 33 dm. Oblicz objętość beczki. Dla ułatwienia obliczeń przyjmij 
. Zapisz obliczenia.
V umiejętność: posługiwanie się językiem symboli i wyrażeń algebraicznych (zapisywanie wielkości za pomocą wyrażeń algebraicznych, przekształcanie wyrażeń algebraicznych, zapisywanie związków między wielkościami za pomocą równań)
Przykład 25 – zapisywanie wyrażeń algebraicznych
W wiadrze jest 
litrów wody, a w garnku 
litrów wody. Ile litrów wody będzie w wiadrze, a ile w garnku, jeśli:
1. z wiadra przelejemy do garnka 1,5 litra wody;
2. przelejemy połowę wody z garnka do wiadra?
Wpisz do tabeli odpowiednie wyrażenia algebraiczne.
Przykład 26 – przekształcanie wyrażeń algebraicznych
Objętość (
) cieczy przepływającej przez rurę o polu przekroju 
oblicza się według wzoru 
, gdzie 
oznacza prędkość przepływu cieczy, 
czas przepływu. Który wzór na prędkość cieczy przepływającej przez rurę jest rezultatem poprawnego przekształcenia podanego wzoru?
A. 
B. 
C. 
D. 
Przykład 27 – układanie równań lub układów równań
Trzy lata temu posadzono przed domem krzew. Co roku podwajał on swoją wysokość i teraz ma 144 cm. Jeśli przez oznaczymy wysokość krzewu w dniu posadzenia, to informacjom z zadania odpowiada równanie:
A. 
B. 
C. 
D. 
Przykład 28 – ułożenie i rozwiązanie równania lub układu równań („zadanie tekstowe”)
Na wycieczkę do Brukseli pojechało 38 uczniów i 4 opiekunów. Zarezerwowano dla nich nocleg w pokojach dwu i trzyosobowych. Cała grupa nocowała w 17 pokojach. Wszystkie zarezerwowane pokoje były w pełni wykorzystane. Ile zarezerwowano pokoi dwuosobowych, a ile trzyosobowych? Zapisz obliczenia.
Przykład 29 – analizowanie podanych funkcji
Obserwując zużycie benzyny w swoim samochodzie pan Nowak stwierdził, że jeśli wystartuje z pełnym bakiem i będzie jechał po autostradzie ze stałą prędkością, to zależność liczby litrów benzyny w baku () od liczby przejechanych kilometrów () wyraża się wzorem
Jaką pojemność ma bak tego samochodu?
Przykład 30 – opisanie funkcji za pomocą wzoru
Most zbudowany jest z przęseł o długości 10 m każde. Przęsło pod wpływem wzrostu temperatury wydłuża się. Przyrost tego wydłużenia jest wprost proporcjonalny do przyrostu temperatury. Wartość przyrostu długości przęsła dla wybranych wartości przyrostu temperatury przedstawia poniższa tabela:
|
przyrost temperatury |
0 |
10 |
30 |
45 |
|
przyrost długości przęsła |
0 |
1 |
3 |
4,5 |
Zapisz zależność długości przęsła (
) od przyrostu temperatury (
) za pomocą wzoru. Podaj współczynnik proporcjonalności do z odpowiednią jednostką.
Przykład 31 – wybranie układu równań odpowiedniego do opisanej sytuacji.
Rodzice Jacka kupili 36 butelek wody mineralnej o pojemnościach 0,5 litra i 1,5 litra. W sumie zakupili 42 litry wody. Przyjmij, że oznacza liczbę butelek o pojemności 0,5 litra, – liczbę butelek o pojemności 1,5 litra. Który układ równań umożliwi obliczenie, ile zakupiono mniejszych butelek wody mineralnej, a ile większych?
A. 
B. 
C.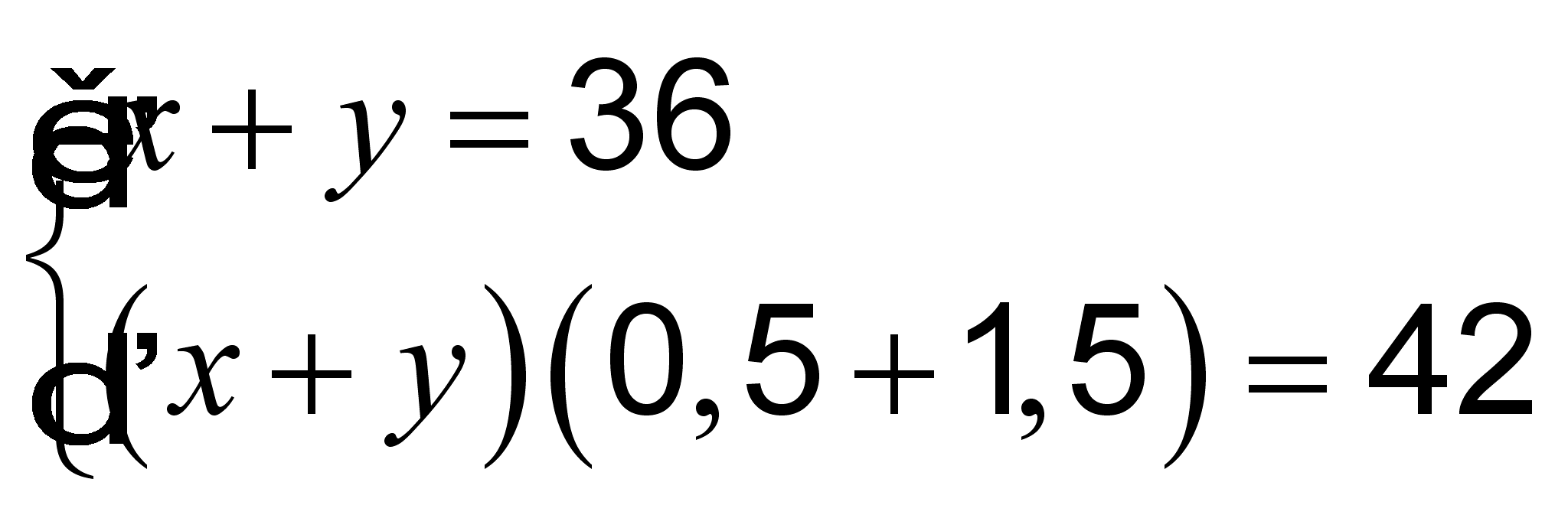 
D. 
Przykład 32 – posługiwanie się językiem symboli chemicznych
Na podstawie informacji z poniższego fragmentu tabeli rozpuszczalności soli i wodorotlenków w wodzie wybierz zdanie prawdziwe.
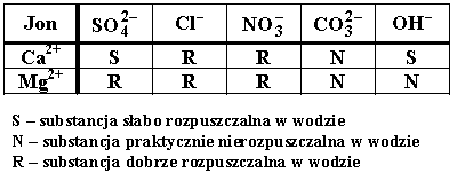
A. Wodorotlenek wapnia słabo rozpuszcza się w wodzie.
B. Wodorotlenek wapnia nie rozpuszcza się w wodzie.
C. W tabeli nie podano informacji o rozpuszczalności wodorotlenku wapnia.
D. Wodorotlenek wapnia dobrze rozpuszcza się w wodzie.
VI umiejętność: stosowanie terminów i pojęć matematyczno – przyrodniczych do opisu zjawisk, właściwości, zachowań, obiektów i organizmów
Przykład 33 – posługiwanie się układem okresowym pierwiastków
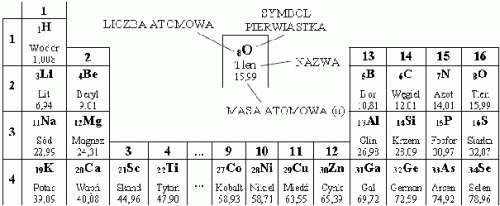
Na podstawie zamieszczonego fragmentu układu ukresowego wybierz zdanie prawdziwe dotyczące sodu 
:
A. W jądrze atomu sodu jest 11 neutronów.
B. Liczba atomowa sodu jest równa 12.
C. Atom sodu ma konfigurację elektronową: 2, 8, 1.
D. Sód leży w trzecim okresie i drugiej grupie układu okresowego.
Przykład 34 – określanie zmian energii
Na fragmencie poziomicowej mapy terenu górskiego zaznaczone są punkty D, G, K, S i W.
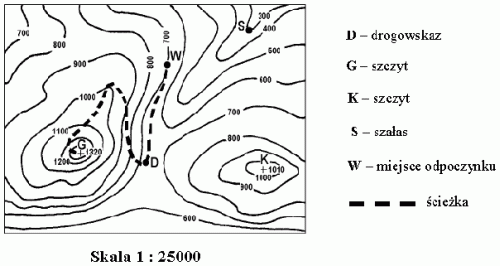
Uczestnicy wycieczki odpoczywający w punkcie W mają pewną energię potencjalną grawitacji. Jak zmieni się ich energia potencjalna grawitacji po wejściu na szczyt G?
A. Zmniejszy się.
B. Zwiększy się.
C. Pozostanie taka sama.
D. Zamieni się na kinetyczną.
Przykład 35 – określanie oddziaływań między organizmami
Określ oddziaływania między populacją mszycy a populacją brzozy.
A. Rywalizują o zasoby środowiska.
B. Obie odnoszą wzajemne korzyści.
C. Nie są zdolne do życia jedna bez drugiej.
D. Jedna z populacji osiąga korzyści, a druga ponosi straty.
Przykład 36 – posługiwanie się skalą mapy
Długość trasy na mapie w skali 1 : 10 000 000 jest równa 7,7 cm. W rzeczywistości trasa ta ma długość
A. 7,7 km
B. 77 km
C. 770 km
D. 7700 km.
Przykład 37 – określanie składu substancji chemicznej
Ile atomów tworzy cząsteczkę wody i ile pierwiastków wchodzi w jej skład?
A. Dwa atomy, trzy pierwiastki.
B. Trzy atomy, dwa pierwiastki.
C. Trzy atomy, jeden pierwiastek.
D. Dwa atomy, dwa pierwiastki.
Przykład 38 – posługiwanie się pojęciami masy i siły
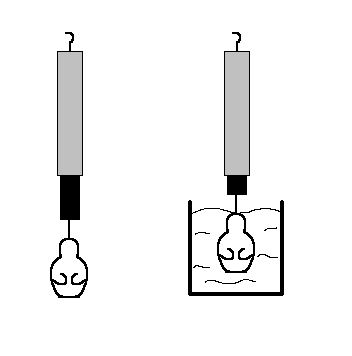
Na siłomierzu zawieszono posążek. Siłomierz wskazywał wtedy wartość 77,3 N. Po zanurzeniu posążka w wodzie wskazanie siłomierza zmniejszyło się do 73 N. Wskaż zdanie prawdziwe.
A. W wodzie masa posążka jest mniejsza niż w powietrzu.
B. W wodzie na posążek działa mniejsza siła grawitacji.
C. W wodzie na posążek oprócz siły grawitacji działa siła wyporu.
D. W wodzie na posążek działa tylko siła wyporu.
Przykład 39 – określanie składników ekosystemu
W ekosystemie wodnym fitoplankton (plankton roślinny) pełni rolę
A. producentów
B. destruentów
C. konsumentów I rzędu
D. konsumentów wyższych rzędów.
Przykład 40 – określanie kierunków geograficznych
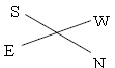
W południe słoneczne drzewo stojące pośrodku ogrodu rzuca cień.
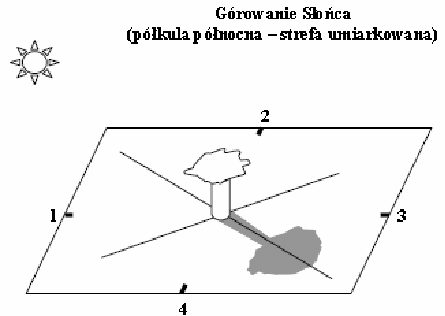
Podpisz w odpowiednich miejscach na rysunku wszystkie główne kierunki geograficzne.
Przykład 41 – określanie stężeń roztworów
Zasolenie Bałtyku wynosi średnio 7,8‰.
Jedna tona średnio zasolonej wody z Morza Bałtyckiego zawiera około
A. 0,078 kg soli
B. 0,78 kg soli
C. 7,8 kg soli
D. 78 kg soli.
Przykład 42 – posługiwanie się własnościami obwodów elektrycznych
Obwód elektryczny składa się z 9 V baterii, amperomierza i trzech identycznych żarówek.
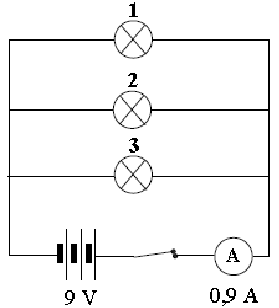
Na podstawie przedstawionego schematu można wnioskować, że
A. żarówka 1 świeci jaśniej niż żarówka 3
B. żarówka 3 świeci jaśniej niż żarówka 1
C. żarówka 2 świeci jaśniej niż żarówki 1 i 3
D. wszystkie żarówki świecą tak samo jasno.
Przykład 43 – opisywanie organizmów
Porosty to organizmy powstające w wyniku symbiozy
A. grzyba i glonu.
B. grzyba i drzewa.
C. grzyba i mchu.
D. dwóch gatunków grzybów.
Przykład 44 – rozpoznawanie formacji roślinnych
Na Ziemi występuje wiele formacji roślinnych, których rozmieszczenie jest w głównej mierze uzależnione od klimatu. Na podstawie opisu rozpoznaj formację roślinną.
Występuje w strefie międzyzwrotnikowej. Rosną tam głównie trawy oraz pojedyncze drzewa, wśród których dominują akacje i baobaby.
A. Tajga
B. Sawanna
C. Step
D. Tundra.
VII umiejętność: stosowanie zintegrowanej wiedzy i umiejętności do rozwiązywania problemów (kojarzenie różnych faktów, wyciąganie wniosków, układanie i realizowanie planu rozwiązania problemu)
Przykład 45 – kojarzenie różnych faktów dotyczących sił działających na ciało
Kropla wody spadająca z chmury poruszała się początkowo ruchem przyspieszonym, a później ruchem jednostajnym. Wybierz rysunki, na których poprawnie przedstawiono siły działające na kroplę wody w początkowej i w końcowej fazie spadania (
oznacza siłę oporu powietrza, 
– siłę ciężkości).
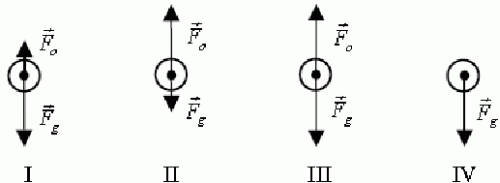
A. Faza początkowa – rysunek II, końcowa – rysunek III
B. Faza początkowa – rysunek I, końcowa – rysunek III
C. Faza początkowa – rysunek II, końcowa – rysunek IV
A. Faza początkowa – rysunek IV, końcowa – rysunek I.
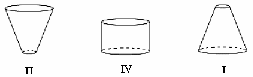
Przykład 46 – powiązanie kształtu bryły z jej objętością
Do początkowo pustych wazonów, takich jak przedstawiono na rysunkach, jednakowym i równomiernym strumieniem wpływała woda.
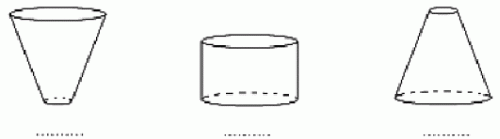
Na wykresach I – IV przedstawiono schematycznie charakter zależności wysokości poziomu wody w wazonie od czasu jego napełniania. Pod każdym wazonem wpisz numer odpowiedniego wykresu.
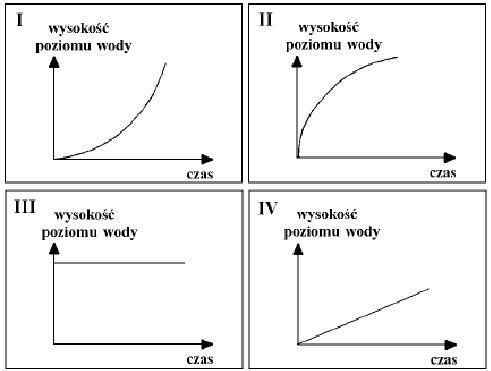
Przykład 47 – obliczanie wartości funkcji opisanej słownie
Na fragmencie poziomicowej mapy terenu górskiego zaznaczone są punkty D, G, K, S i W.
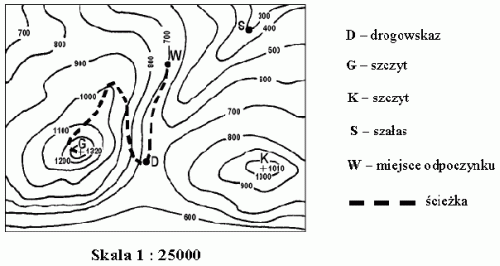
Reguła obliczania czasu przejścia trasy w górach:
Przyjmij 1 godzinę na każde 5 km odczytane (w poziomie) z mapy i dodaj po 1 godzinie na każde 600 m wzniesienia, które trzeba pokonać.
Ścieżka prowadząca od punktu W na szczyt G ma na mapie długość 10 cm. Zgodnie z powyższą regułą wejście tą trasą na szczyt zajmie uczestnikom wycieczki około
A. 1 h
B. 1,5 h
C. 2 h
D. 3 h.
Przykład 48 – określanie zagrożeń dla środowiska
W okresie wiosennym niektórzy rolnicy mimo zakazu wypalają trawę. Podaj dwa negatywne dla środowiska skutki takiego działania.
Przykład 49 – kojarzenie wyników doświadczeń i wyciąganie wniosków
Tomek wykonał doświadczenie, w którym na cynk podziałał kwasem solnym. Probówkę do zbierania wydzielającego się gazu umieścił w wanience z wodą. Rysunek przedstawia schemat tego doświadczenia.
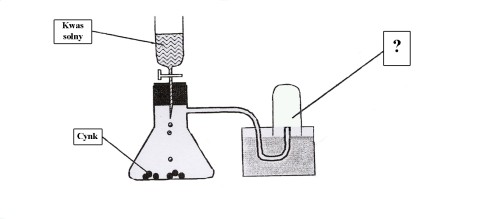
a) Zapisz równanie reakcji zachodzącej w doświadczeniu.
b) Nazwij powstałe produkty reakcji, uzupełniając zdanie:
Produktami reakcji zachodzącej w doświadczeniu są ………………………………….
c) Napisz, w jaki sposób zidentyfikujesz wydzielający się gaz.
{mospagebreak title=Odpowiedzi&heading=Pytania}
Odpowiedzi do umiejętności
- 1. A
- 2. A
- 3. Ze wzrostem temperatury rozpuszczalność soli rośnie, a gazów maleje. W 100 g wody o temperaturze 500C można rozpuścić co najwyżej 30 g NH3.
- 4. A
- 5. B
- 6. C
- 7. B
- 8. B
- 9. B
- 10. C
- 11. Konsumenci I rzędu (mszyce) broniąc się przed naturalnymi wrogami wydzielają obronną ciecz.
- 12. Po 8 miesiącach.
- 13.
- 14. C
- 15. C
- 16. Godzina 19.08
- 17. C
- 18. A
- 19. 3,84 zł
- 20. C
- 21. A
- 22. Trzeba wyłożyć gliną 1300 m2 powierzchni wału.
- 23.
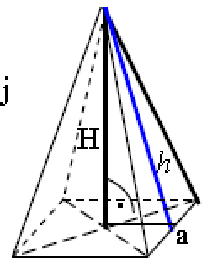Powierzchnia ścian bocznych jest równa 1500 m2. - 24. Beczka ma objętość 847 dm3.
- 25.
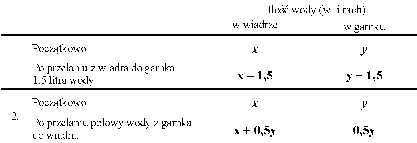
- 26. A
- 27. C
- 28. Zarezerwowano 9 pokoi dwuosobowych i 8 pokoi trzyosobowych.
- 29. 45 litrów.
- 30.
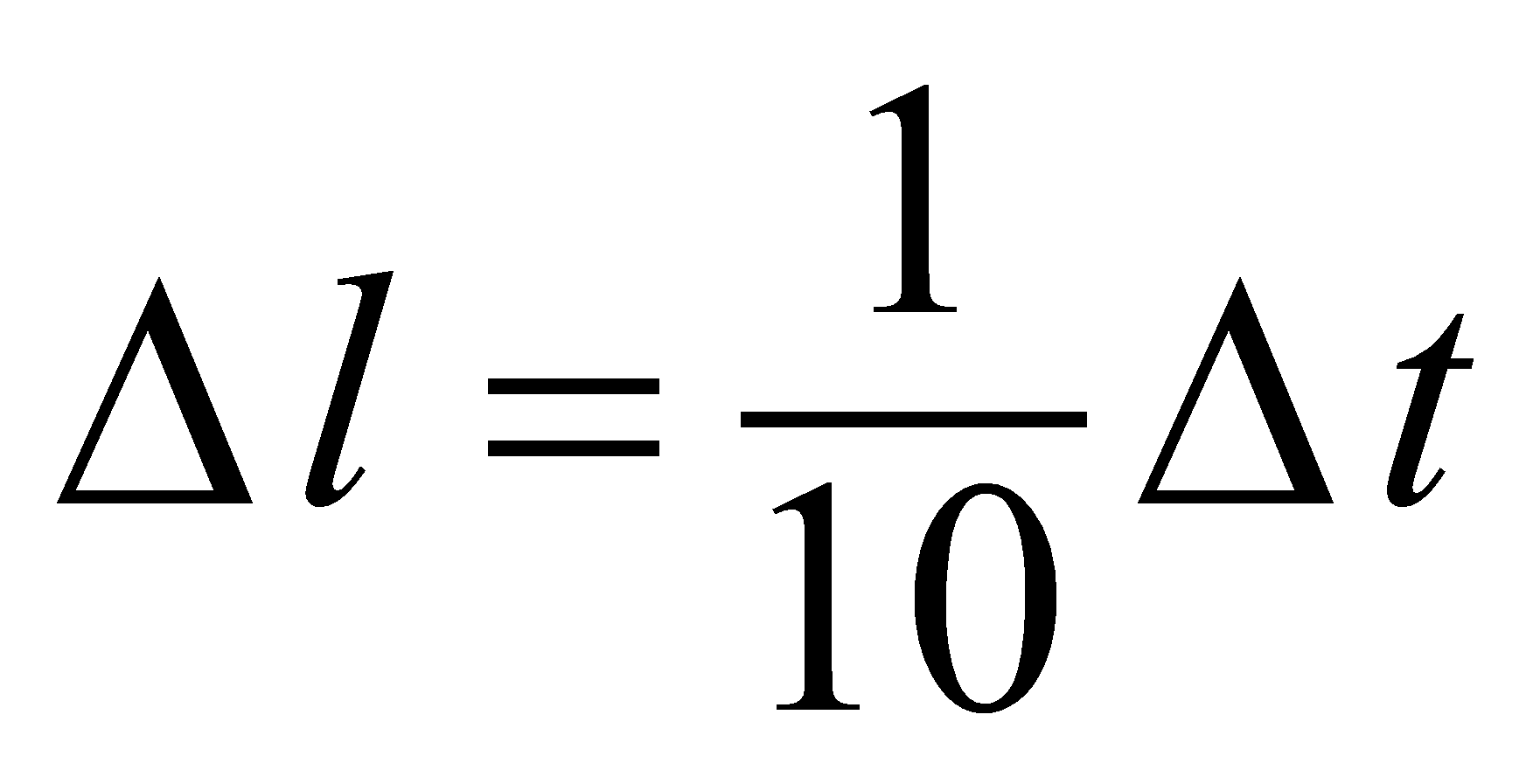, współczynnik: 
- 31. B
- 32. A
- 33. C
- 34. B
- 35. D
- 36. C
- 37. B
- 38. C
- 39. A
- 40.
- 41. C
- 42. D
- 43. A
- 44. B
- 45. B
- 46.
- 47. B
- 48. Należy podać dwie spośród następujących odpowiedzi:
- Niszczy się organizmy żywe.
- Rozprzestrzenia się pożar.
- Do atmosfery jest emitowany CO2.
- 49. a) Zn + 2 HCl
ZnCl2 + H2↑
- b) chlorek cynku, wodór
- c) włożenie do probówki z gazem żarzącego (palącego) się łuczywa, gaz spali się
z charakterystycznym odgłosem – trzaskiem, pyknięciem.
Sprawdź kursy przygotowawcze w Warszawie – www.marka.edu.pl